题目内容
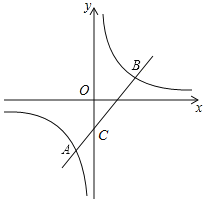
【题目】如图,一次函数y=k1x+b(k1≠0)与反比例函数y=![]() (k2≠0)的图象交于A(-1,-4)和点B(4,m)
(k2≠0)的图象交于A(-1,-4)和点B(4,m)
(1)求这两个函数的解析式;
(2)已知直线AB交y轴于点C,点P(n,0)在x轴的负半轴上,若△BCP为等腰三角形,求n的值.
【答案】(1)反比例函数解析式为y=![]() ,一次函数的解析式为y=x-3;(2)满足条件的n为-
,一次函数的解析式为y=x-3;(2)满足条件的n为-![]() 或(4-
或(4-![]() ).
).
【解析】
(1)先将点A坐标代入反比例函数解析式中求出k2,进而求出点B坐标,最后将点A,B坐标代入一次函数解析式中,即可得出结论;
(2)利用两点间的距离公式表示出BC2=32,CP2=n2+9,BP2=(n-4)2+1,再分三种情况利用两腰相等建立方程求解即可得出结论.
(1)∵点A(-1,-4)在反比例函数y=![]() (k2≠0)的图象上,
(k2≠0)的图象上,
∴k2=-1×(-4)=4,
∴反比例函数解析式为y=![]() ,
,
将点B(4,m)代入反比例函数y=![]() 中,得m=1,
中,得m=1,
∴B(4,1),
将点A(-1,-4),B(4,1)代入一次函数y=k1x+b中,得
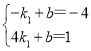 ,
,
∴![]() ,
,
∴一次函数的解析式为y=x-3;
(2)由(1)知,直线AB解析式为y=x-3,
∴C(0,-3),
∵B(4,1),P(n,0),
∴BC2=32,CP2=n2+9,BP2=(n-4)2+1,
∵△BCP为等腰三角形,
∴①当BC=CP时,
∴32=n2+9,
∴n=![]() (舍)或n=-
(舍)或n=-![]() ,
,
②当BC=BP时,32=(n-4)2+1,
∴n=4+![]() (舍)或n=4-
(舍)或n=4-![]() ,
,
③当CP=BP时,n2+9=(n-4)2+1,
∴n=1(舍),
即:满足条件的n为-![]() 或(4-
或(4-![]() ).
).

 教学练新同步练习系列答案
教学练新同步练习系列答案【题目】在生活中,有很多函数并不一定存在解析式,对于这样的函数,我们可以通过列表和图象来对它可能存在的性质进行探索,例如下面这样一个问题:
已知y是x的函数,下表是y与x的几组对应值.
x | … | ﹣5 | ﹣4 | ﹣3 | ﹣2 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 1.969 | 1.938 | 1.875 | 1.75 | 1 | 0 | ﹣2 | ﹣1.5 | 0 | 2.5 | … |
小孙同学根据学习函数的经验,利用上述表格反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
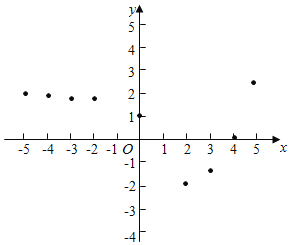
下面是小孙同学的探究过程,请补充完整;
(1)如图,在平面之间坐标系xOy中,描出了以上表中各对应值为坐标的点,根据描出的点,画出函数的图象:
(2)根据画出的函数图象回答:
①x=﹣1时,对应的函数值y的为 ;
②若函数值y>0,则x的取值范围是 ;
③写出该函数的一条性质(不能与前面已有的重复): .