题目内容
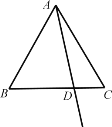
【题目】如图一块直角三角形ABC,∠B=90°,AB=3,BC=4,截得两个正方形DEFG,BHJN,设S1=DEFG的面积,S2=BHJN的面积,则S1、S2的大小关系是( )
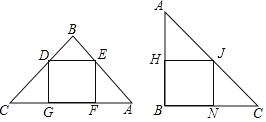
A.S1>S2B.S1<S2C.S1=S2D.不能确定
【答案】B
【解析】
根据勾股定理求出AC,求出AC边上的高BM,根据相似三角形的性质得出方程,求出方程的解,即可求得S1,如图2,根据相似三角形的性质列方程求得HJ=![]() ,于是得到S2=(
,于是得到S2=(![]() )2>(
)2>(![]() )2,即可得到结论.
)2,即可得到结论.
解:如图1,设正方形DEFG的边长是x,
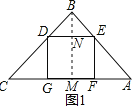
∵△ABC是直角三角形,∠B=90°,AB=3,BC=4,
∴由勾股定理得:AC=5,
过B作BM⊥AC于M,交DE于N,
由三角形面积公式得:![]() BC×AB=
BC×AB=![]() AC×BM,
AC×BM,
∵AB=3,AC=5,BC=4,
∴BM=2.4,
∵四边形DEFG是正方形,
∴DG=GF=EF=DE=MN=x,DE∥AC,
∴△BDE∽△ABC,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴x=![]() ,
,
即正方形DEFG的边长是![]() ;
;
∴S1=(![]() )2,
)2,
如图2,
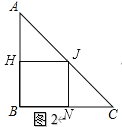
∵HJ∥BC,
∴△AHJ∽△ABC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴HJ=![]() ,
,
∴S2=(![]() )2>(
)2>(![]() )2,
)2,
∴S1<S2,
故选:B.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目