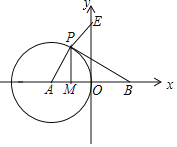Question

【题目】已知一次函数y＝kx+3﹣2k，A（﹣2，1），B（1，﹣3），C（﹣2，﹣3）

（1）说明点M（2，3）在直线y＝kx+3﹣2k上；

（2）当直线y＝kx+3﹣2k经过点C时，点P是直线y＝kx+3﹣2上一点，若S△BCP＝2S△ABC，求点P的坐标．

Answer 1

【答案】（1）见解析；（2）点P的坐标为（﹣，﹣11）或（，5）

【解析】

（1）将x=2代入y=kx+3-2k，求出y=3，由此即可证出点M（2，3）在直线y=kx+3-2上；
（2）根据点C的坐标利用待定系数法求出此时直线的解析式，由此可设点P的坐标为（m，m），再根据S△BCP=2S△ABC，即可得出关于m的含绝对值符号的一元一次方程，解方程求出m的值，将其代入P点坐标即可得出结论．

（1）证明：∵y＝kx+3﹣2k，

∴当x＝2时，y＝2k+3﹣2k＝3，

∴点M（2，3）在直线y＝kx+3﹣2k上；

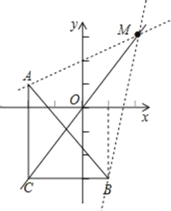
（2）解：将点C（﹣2，﹣3）代入y＝kx+3﹣2k，

得：﹣3＝﹣2k+3﹣2k，解得：k＝，

此时直线CM的解析式为y＝x．

设点P的坐标为（m，m）．

∵S△BCP＝BC|yP﹣yB|，S△ABC＝BC|yA﹣yC|，S△BCP＝2S△ABC，

∴|m﹣（﹣3）|＝2×[1﹣（﹣3）]，

解得：m1＝﹣，m2＝，

∴点P的坐标为（﹣，﹣11）或（，5）．