题目内容
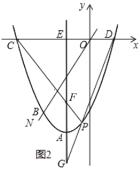
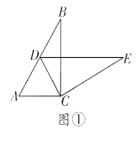
【题目】如图1,点P是平面内任意一点,点A,B是![]() 上不重合的两个点,连结
上不重合的两个点,连结![]() .当
.当![]() 时,我们称点P为
时,我们称点P为![]() 的“关于
的“关于![]() 的关联点”.
的关联点”.

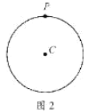
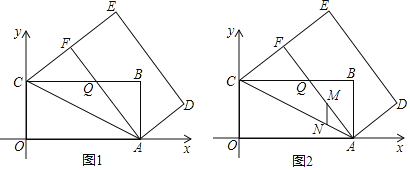
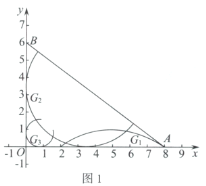
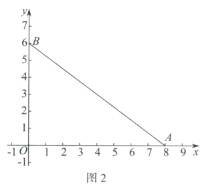
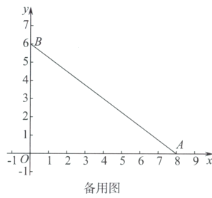
(1)如图2,当点P在![]() 上时,点P是
上时,点P是![]() 的“关于
的“关于![]() 的关联点”时,画出一个满足条件的
的关联点”时,画出一个满足条件的![]() ,并直接写出
,并直接写出![]() 的度数;
的度数;
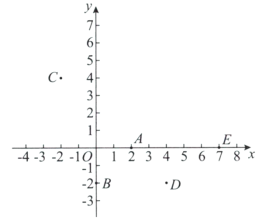
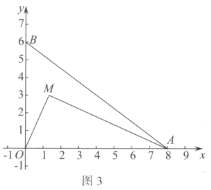
(2)在平面直角坐标系中有点![]() ,点M关于y轴的对称点为点N.
,点M关于y轴的对称点为点N.
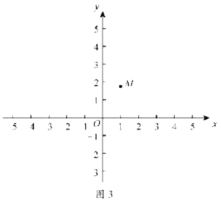
①以点O为圆心,![]() 为半径画
为半径画![]() ,在y轴上存在一点P,使点P为
,在y轴上存在一点P,使点P为![]() “关于
“关于![]() 的关联点”,直接写出点P的坐标;
的关联点”,直接写出点P的坐标;
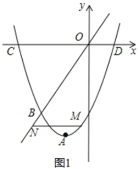
②点![]() 是x轴上一动点,当
是x轴上一动点,当![]() 的半径为1时,线段
的半径为1时,线段![]() 上至少存在一点是
上至少存在一点是![]() 的“关于某两个点的关联点”,求m的取值范围.
的“关于某两个点的关联点”,求m的取值范围.
【答案】(1)详见解析;(2)①![]() 或
或![]() ;②
;②![]()
【解析】
(1)由题意当点P在在![]() 上时,点P是
上时,点P是![]() 的“关于
的“关于![]() 的关联点”时,则圆心角∠ACB=120°,由此作图即可;
的关联点”时,则圆心角∠ACB=120°,由此作图即可;
(2)①设点P(0,y),连接MP,NP,MN交y轴于点Q,由题意及对称性可得△PMN为等边三角形,然后根据锐角三角函数值求PQ的长,从而确定点P的坐标;
②考虑临界情况,即恰好M、N点为⊙D的关联时,确定点D的坐标,从而求其取值范围.
解:(1)补全图形
由题意可知,∠APB=60°,点P在圆上
∴∠ACB=120°

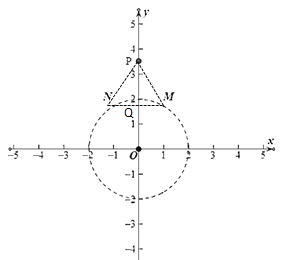
(2)①设点P(0,y),连接MP,NP,MN交y轴于点Q
由题意可知,∠MPN=60°
又∵点M关于y轴的对称点为点N
∴△PMN为等边三角形
∴在Rt△MPQ中,![]()
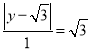 ,解得:
,解得:![]() 或0
或0
∴![]() 或
或![]()
②当点D位于M点右侧且点M在圆上时,此时m有最大值,
由题意可知,此时∠OMD=60°,∴m=2
当点D位于N点左侧且点N在圆上时,此时m有最小值,
由题意可知,此时∠OMD=60°,∴m=-2
∴![]()


练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目