题目内容
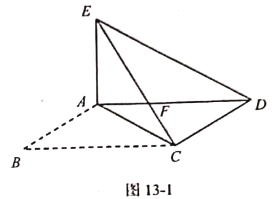
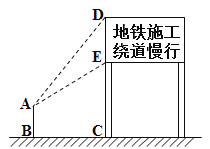
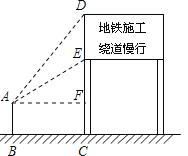
【题目】某市地铁工程正在加快建设,为了缓解市区内一些主要路段交通拥挤的现状,交警大队在一些主要路口设立了交通路况指示牌,如图所示,小明在离指示牌3.2米的点B处测得指示牌顶端D点和底端E点的仰角分别为52°和30°.求路况指示牌DE的高度.(精确到0.01米,参考数据:![]() ≈1.732,sin52°≈0.79,cos52°≈0.62, tan52°≈1.28.)
≈1.732,sin52°≈0.79,cos52°≈0.62, tan52°≈1.28.)
【答案】路况指示牌DE的高度约为2.25米.
【解析】
过点A作AF⊥DC于点F,在Rt△ADF中求出DF,在Rt△AEF中求出EF,继而根据DE=DF-EF,可得出答案.
解:过点A作AF⊥DC于点F,
在Rt△ADF中,AF=3.2,tan∠DAF=tan52°=![]() ,
,
∴DF=AFtan52°=3.2×1.28≈4.10米.
在Rt△AEF中,AF=3.2,tan∠EAF=tan30°=![]() ,
,
∴EF=AFtan30°=3.2×0.577≈1.85米.
故可得DE=DF﹣EF=2.25米.
答:路况指示牌DE的高度约为2.25米.

练习册系列答案
相关题目
【题目】如图,正方形ABCD内部有若干个点,则用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):
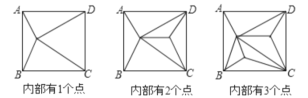
(1)填写下表:
正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | ... | n |
分割成三角形的个数 | 4 | 6 | _____ | _____ | ... | _____ |
(2)原正方形能否被分割成2021个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.