题目内容

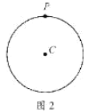
【题目】如图，一艘海轮位于灯塔P的北偏东65°方向，距离灯塔80海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东45°方向上的B处，则这时海轮所在的B处距离灯塔P的距离是( )

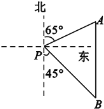
A.B.C.D.

【答案】C

【解析】

如图，过点P作PD⊥AB于点D，首先根据题意得出∠MPA=∠A=65°，以及∠DBP=∠DPB=45°，再利用解直角三角形求出即可．

解：如图，过点P作PD⊥AB于点D

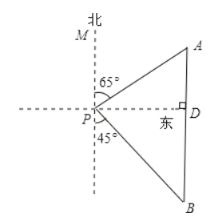
由题意知∠DBP=∠DPB=45°

在Rt△PBD中，cos∠DPB=

即cos45°==

∴PB=PD

∵点A在点P的北偏东65°方向上

∴∠APD=25°

在Rt△PAD中，cos25°=

∴PD=PAcos25°=80cos25°

∴PB=80 cos25°（海里）

故选C．

练习册系列答案
相关题目

【题目】如图，在中，动点从点出发，在边上以每秒的速度向点匀速运动，同时动点从点出发，在边上以每秒的速度向点匀速运动，运动时间为秒，连接．若以为直径的与的边相切，则的值为_______．

【题目】如图，Rt△AOB中，∠AOB=90°，，顶点A在反比例函数则点B所在的反比例函数解析式为_________．

【题目】在疫情防控期间，某中学为保障广大师生生命健康安全购进一批免洗手消毒液和84消毒液．如果购买100瓶免洗手消毒液和150瓶84消毒液，共需花费1500元；如果购买120瓶免洗手消毒液和160瓶84消毒液，共需花费1720元．

（1）每瓶免洗手消毒液和每瓶84消毒液的价格分别是多少元？

（2）某药店出售免洗手消毒液，满150瓶免费赠送10瓶84消毒液．若学校从该药店购进免洗手消毒液和84消毒液共230瓶，恰好用去1700元，则学校购买免洗手消毒液多少瓶?

【题目】某中学对该校学生进行了“你喜欢的运动项目”的情况问卷调查，在全部调查问卷中，随机抽取了部分学生的调查问卷进行了分析整理，得到了如下的样本统计图表和扇形统计图:

　　　　

(1)求m，n的值；

(2)该校学生总数为500人，学校决定按比例在B，C，D类学生中抽取学生进行课余训练，其比例为B类20%，C，D类各取60%，请你估计该校参加课余训练的学生数；

(3)随机抽取的部分学生的调查问卷中,若C类运动项目的4位学生中有3位男生，1位女生，请用列举法求出在C类中随机抽出2位学生进行专家培训，其中有1位女生的概率．

【题目】如图①，四边形中，，，从点出发，以每秒2个单位长度的速度，按的顺序在边上匀速运动，设点的运动时间为秒，的面积为，关于的函数图像如图②所示，当运动到中点时，的面积为__________．

【题目】如图①，在平面直角坐标系中，抛物线y＝ax2＋bx＋c（a≠0）经过点D（2，4），与x轴交于A，B两点，与y轴交于点C（0，4），连接AC，CD，BC， 其且AC=5．

（1）求抛物线的解析式；

（2）如图②，点P是抛物线上的一个动点，过点P作x轴的垂线l，l分别交x轴于点E，交直线AC于点M．设点P的横坐标为m．当0<m≤2时，过点M作MG∥BC，MG交x轴于点G，连接GC，则m为何值时，△GMC的面积取得最大值，并求出这个最大值；

（3）当-1<m≤2时，是否存在实数m，使得以P，C，M为顶点的三角形和△AEM相似？若存在，求出相应m的值；若不存在，请说明理由．

【题目】如图1，点P是平面内任意一点，点A，B是上不重合的两个点，连结．当时，我们称点P为的“关于的关联点”．

（1）如图2，当点P在上时，点P是的“关于的关联点”时，画出一个满足条件的，并直接写出的度数；

（2）在平面直角坐标系中有点，点M关于y轴的对称点为点N．

①以点O为圆心，为半径画，在y轴上存在一点P，使点P为“关于的关联点”，直接写出点P的坐标；

②点是x轴上一动点，当的半径为1时，线段上至少存在一点是的“关于某两个点的关联点”，求m的取值范围．

【题目】如图，正方形ABCD内部有若干个点，则用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形（互相不重叠）：

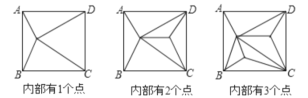
（1）填写下表：

正方形ABCD内点的个数

1

2

3

4

．．．

n

分割成三角形的个数

4

6

_____

_____

．．．

_____

（2）原正方形能否被分割成2021个三角形？若能，求此时正方形ABCD内部有多少个点？若不能，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网