题目内容
【题目】综合与实践
问题情境
数学活动课上,老师让同学们以“三角形的旋转”为主题开展数学活动,![]() 和
和![]() 是两个全等的直角三角形纸片,其中
是两个全等的直角三角形纸片,其中![]() ,
,![]() ,
,![]() .
.
解决问题
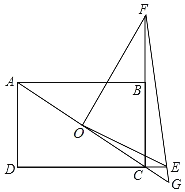
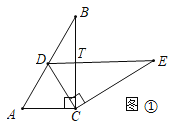
(1)如图①,智慧小组将![]() 绕点
绕点![]() 顺时针旋转,发现当点
顺时针旋转,发现当点![]() 恰好落在
恰好落在![]() 边上时,
边上时,![]() ,请你帮他们证明这个结论;
,请你帮他们证明这个结论;
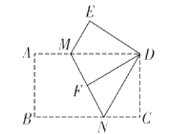
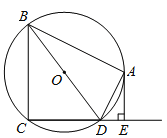
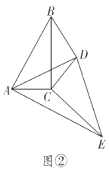
(2)缜密小组在智慧小组的基础上继续探究,连接![]() ,当
,当![]() C绕点
C绕点![]() 继续旋转到如图②所示的位置时,他们提出
继续旋转到如图②所示的位置时,他们提出![]() ,请你帮他们验证这一结论是否正确,并说明理由;
,请你帮他们验证这一结论是否正确,并说明理由;
探索发现
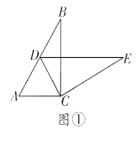
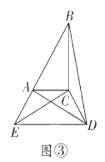
(3)如图③,勤奋小组在前两个小组的启发下,继续旋转![]() ,当
,当![]() 三点共线时,求
三点共线时,求![]() 的长;
的长;
(4)在图①的基础上,写出一个边长比为![]() 的三角形(可添加字母).
的三角形(可添加字母).
【答案】(1)详见解析;(2)正确,理由详见解析;(3)![]() ;(4)答案不唯一,合理即可.
;(4)答案不唯一,合理即可.
【解析】
(1)如图①中,根据旋转的性质可得AC=CD,然后求出△ACD是等边三角形,根据等边三角形的性质可得∠ACD=60°,然后根据内错角相等,两直线平行进行解答;
(2)如图②中,作DM⊥BC于M,AN⊥EC交EC的延长线于N.根据旋转的性质可得BC=CE,AC=CD,再求出∠ACN=∠DCM,然后利用“角角边”证明△ACN和△DCM全等,根据全等三角形对应边相等可得AN=DM,然后利用等底等高的三角形的面积相等证明.
(3)如图③中,作CH⊥AD于H.解直角三角形求出AD,证明∠BAD=90°,利用勾股定理即可解决问题.
(4)根据含有30°的直角三角形的三边之比为1:![]() :2求解即可.
:2求解即可.
(1)如图①中,∵△DEC绕点C旋转点D恰好落在AB边上,
∴AC=CD,
∵∠BAC=90°-∠B=90°-30°=60°,
∴△ACD是等边三角形,
∴∠ACD=60°,
又∵∠CDE=∠BAC=60°,
∴∠ACD=∠CDE,
∴DE∥AC;
(2)如图②中,作DM⊥BC于M,AN⊥EC交EC的延长线于N.

∵△DEC是由△ABC绕点C旋转得到
∴BC=CE,AC=CD,
∵∠ACN+∠BCN=90°,∠DCM+∠BCN=180°-90°=90°,
∴∠ACN=∠DCM,
在△ACN和△DCM中,
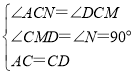 ,
,
∴△ACN≌△DCM(AAS),
∴AN=DM,
∴△BDC的面积和△AEC的面积相等(等底等高的三角形的面积相等),
即S△BDC=S△AEC.
(3)如图③中,作CH⊥AD于H.
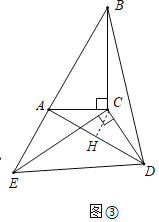
∵,
∵B,A,E共线,
∴∠BAC+∠EAC=180°,
∴∠EAC=120°,
∵∠EDC=60°,
∴∠EAC+∠EDC=180°,
∴A,E,D,C四点共圆,
∴∠CAD=∠CED=30°,∠BAD=90°,
∵CA=CD,CH⊥AD,AC=CD=![]() AB=2
AB=2
∴AH=DH=ACcos30°=![]() ,
,
∴AD=2![]() ,
,
∴![]() .
.
(4)如图①中,设DE交BC于T.
因为含有30°的直角三角形的三边之比为1:![]() :2,
:2,
由(1)可知△BDT,△DCT,△ECT都是含有30°的直三角形,
∴△BDT,△DCT,△ECT符合条件.

【题目】如图,正方形ABCD内部有若干个点,则用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):
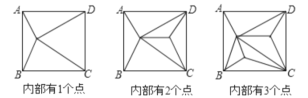
(1)填写下表:
正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | ... | n |
分割成三角形的个数 | 4 | 6 | _____ | _____ | ... | _____ |
(2)原正方形能否被分割成2021个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.