题目内容
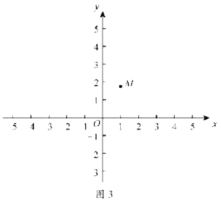
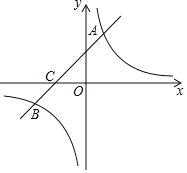
【题目】如图,在平面直角坐标系![]() 中,有五个点
中,有五个点![]() ,将二次函数
,将二次函数![]() 的图象记为W.下列的判断中
的图象记为W.下列的判断中
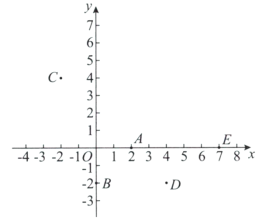
①点A一定不在W上;
②点B,C,D可以同时在W上;
③点C,E不可能同时在W上.
所有正确结论的序号是_________.
【答案】①②
【解析】
由m≠0可得点A 不在抛物线上,故可判断①;先根据B,C两点坐标求出函数关系式,再把D点坐标代入即可判断点D是否在函数图象上;将C、E两点坐标代入![]() ,能求出a,m则可判断出C、E均在函数图象上,否则,则不在函数图象上.
,能求出a,m则可判断出C、E均在函数图象上,否则,则不在函数图象上.
由二次函数![]() 知其顶点坐标为(2,m),而m≠0,
知其顶点坐标为(2,m),而m≠0,
故(2,0)不在函数图象上,
所以,点A不在函数图象上,即点A一定不在W上,故①正确;
把C(-2,4),B(0,-2)代入![]() 得,
得,
![]() ,
,
解得,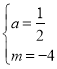 ,
,
∴![]()
当x=4时,y=-2,
所以,点D在函数![]() 的图象上,
的图象上,
因此,点B,C,D可以同时在W上,故②正确;
把C(-2,4),E(7,0)分别代入![]() 得,
得,
![]() ,
,
解得,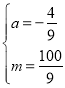
∴![]()
所以,点C,E可能同时在W上,故③错误.
故答案为:①②.

练习册系列答案
 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
【题目】某公司经过市场调查,发现某种运动服的销量与售价是一次函数关系,具体信息如下表:
售价(元/件) | 200 | 210 | 220 | 230 | … |
月销量(件) | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件150元.
(1)售价为![]() 元,月销量为
元,月销量为![]() 件;
件;
①求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
②若销售该运动服的月利润为![]() 元,求
元,求![]() 关于
关于![]() 的函数关系式,并求月利润最大时的售价;
的函数关系式,并求月利润最大时的售价;
(2)由于运动服进价降低了![]() 元,商家决定回馈顾客,打折销售,这时月销量与调整后的售价仍满足(1)中函数关系式.结果发现,此时月利润最大时的售价比调整前月利润最大时的售价低15元,则
元,商家决定回馈顾客,打折销售,这时月销量与调整后的售价仍满足(1)中函数关系式.结果发现,此时月利润最大时的售价比调整前月利润最大时的售价低15元,则![]() 的值是多少?
的值是多少?