题目内容
【题目】在平面内,对于给定的![]() ,如果存在一个半圆或优弧与
,如果存在一个半圆或优弧与![]() 的两边相切,且该弧上的所有点都在
的两边相切,且该弧上的所有点都在![]() 的内部或边上,则称这样的弧为
的内部或边上,则称这样的弧为![]() 的内切弧.当内切弧的半径最大时,称该内切弧为
的内切弧.当内切弧的半径最大时,称该内切弧为![]() 的完美内切弧.(注:弧的半径指该弧所在圆的半径)
的完美内切弧.(注:弧的半径指该弧所在圆的半径)
在平面直角坐标系![]() 中,
中,![]() .
.
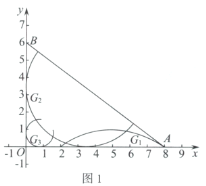
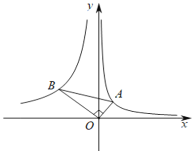
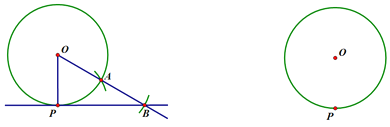
(1)如图1,在弧![]() ,弧
,弧![]() ,弧
,弧![]() 中,是
中,是![]() 的内切弧的是____________;
的内切弧的是____________;
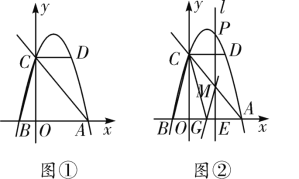
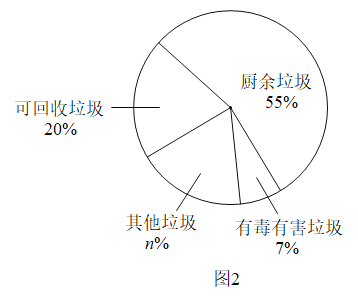
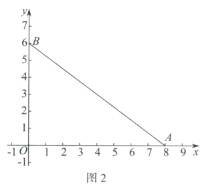
(2)如图2,若弧G为![]() 的内切弧,且弧G与边
的内切弧,且弧G与边![]() 相切,求弧G的半径的最大值;
相切,求弧G的半径的最大值;
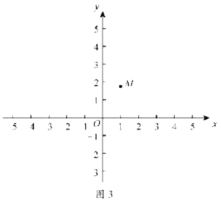
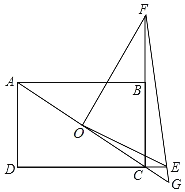
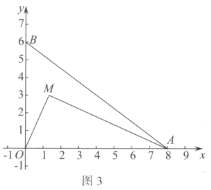
(3)如图3,动点![]() ,连接
,连接![]() .
.
①直接写出![]() 的完美内切弧的半径的最大值;
的完美内切弧的半径的最大值;
②记①中得到的半径最大时的完美内切弧为弧T.点P为弧T上的一个动点,过点P作x轴的垂线,分别交x轴和直线![]() 于点D,E,点F为线段
于点D,E,点F为线段![]() 的中点,直接写出线段
的中点,直接写出线段![]() 长度的取值范围.
长度的取值范围.
【答案】(1)弧![]() ,弧
,弧![]() .(2)3. (3)①
.(2)3. (3)①![]() . ②
. ②![]() 且
且![]() .
.
【解析】
(1)根据内切弧定义即可解答;
(2)由内切弧定义可知弧G所在圆的圆心上![]() 的角平分线
的角平分线![]() 上,弧G的半径最大时其圆心I在
上,弧G的半径最大时其圆心I在![]() 的边
的边![]() 上.再由勾股定理即可计算出半径最大值;
上.再由勾股定理即可计算出半径最大值;
解:(1)由图可知,弧![]() 是半圆,弧
是半圆,弧![]() 是优弧,它们与
是优弧,它们与![]() 的两边相切,且该弧上的所有点都在
的两边相切,且该弧上的所有点都在![]() 的内部或边上,故弧
的内部或边上,故弧![]() ,弧
,弧![]() 是
是![]() 的内切弧;而弧
的内切弧;而弧![]() 只与一边相切,而且是劣弧,故弧
只与一边相切,而且是劣弧,故弧![]() 不是
不是![]() 的内切弧;,
的内切弧;,
弧![]() ,弧
,弧![]() .
.
(2)∵弧G为![]() 的内切弧,且弧G与边
的内切弧,且弧G与边![]() 相切,
相切,
∴弧G所在圆的圆心上![]() 的角平分线
的角平分线![]() 上.
上.
易知若弧G的半径最大,则弧G所在圆的圆心I在![]() 的边
的边![]() 上.设弧G与边
上.设弧G与边![]() 相切分别切于点O,H.
相切分别切于点O,H.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
在![]() 中,
中,![]() ,即
,即![]() .
.
解得![]() .
.
(3)①![]() 的完美内切弧半径的最大值为
的完美内切弧半径的最大值为![]() .
.
理由如下:由内切弧定义可知,内切弧的圆心在相切两边的夹角的角平分线上,而完美内切弧的圆心在最大内角的角平分线与其对边的交点上,
动点![]() 在
在![]() ,
,
∵![]() ,
,
则有![]() 垂直平分OB,
垂直平分OB,
∴MO=MB,
∴MB+MA=MO+MA.
根据两点之间线段最短可得:当B、M、A三点共线时,即M点在AB的中点(4,3),MO+MA取到最小值,最小值为AB长=10.
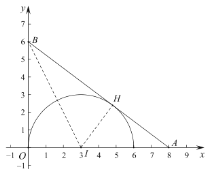
I.当内切弧与OM、MA相切时,如图: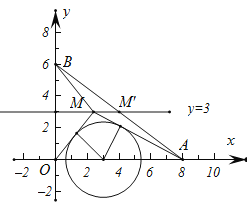
设![]() 的完美内切弧半径为r,
的完美内切弧半径为r,
∵![]() ,
,
∴![]()
∴![]() .
.
当MO+MA取最小值10时,此时r取到最大值,最大值为![]() .
.
II.当完美内切弧与OM、OA相切时,或与MA、OA相切时,相切两边的和为:![]() ,
,![]() ,
,
同理可知,这两种情况的内切弧的半径最大值小于完美内切弧与OM、MA相切时的半径.
综上所述:![]() 的完美内切弧是内切弧与OM、MA相切时的半径的最大值为
的完美内切弧是内切弧与OM、MA相切时的半径的最大值为![]()
②线段![]() 长度的取值范围是
长度的取值范围是![]() 且
且![]() .
.
由①可知:![]() 的完美内切弧的圆心O坐标为(4,0),半径为
的完美内切弧的圆心O坐标为(4,0),半径为![]() ,
,
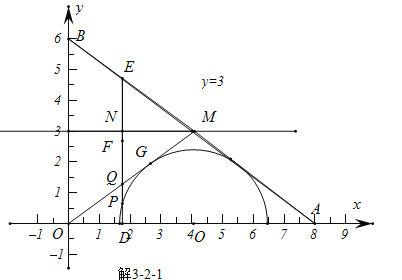
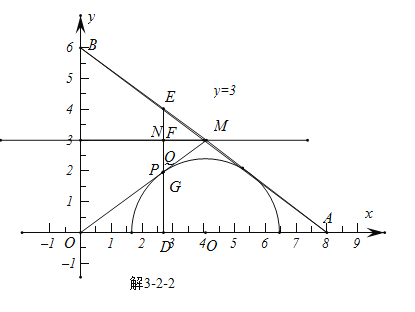
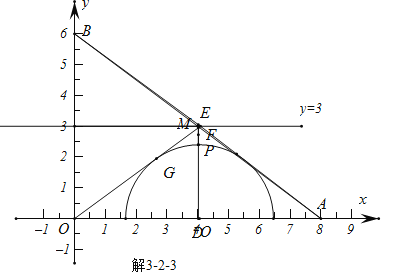

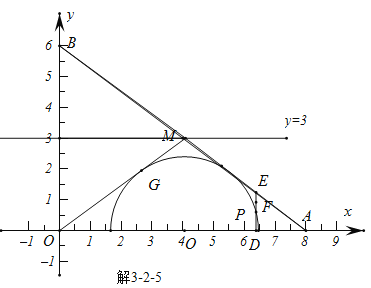
由图解3-2-1,解3-2-2,解3-2-3,解3-2-4,可知,当DE经过切点Q的时候,DF最大为3;
由图解3-2-5可知,当DE与半圆右侧相切的时候,DF最小为![]() ;
;
而当ED经过AB与半圆相切的切点时,此时F点不存在,DF=![]() ,
,
∴线段![]() 长度的取值范围是
长度的取值范围是![]() 且
且![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】如图,正方形ABCD内部有若干个点,则用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):
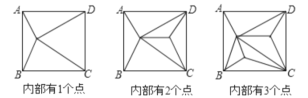
(1)填写下表:
正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | ... | n |
分割成三角形的个数 | 4 | 6 | _____ | _____ | ... | _____ |
(2)原正方形能否被分割成2021个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.