��Ŀ����
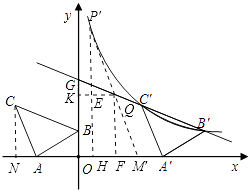
����Ŀ����ͼ����ƽ��ֱ������ϵ����Rt��ABC����A=90�㣬AB=AC��A����2��0����B��0��1����C��d��2����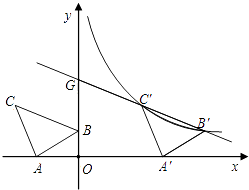
��1����d��ֵ��
��2������ABC��x���������ƽ�ƣ��ڵ�һ������B��C����Ķ�Ӧ��B�䡢C����������ij����������ͼ���ϣ��������������������ʹ�ʱ��ֱ��B��C��Ľ���ʽ��
��3���ڣ�2���������£�ֱ��BC��y���ڵ�G�����Ƿ����x���ϵĵ�M�ͷ���������ͼ���ϵĵ�P��ʹ���ı���PGMC����ƽ���ı��Σ�������ڣ��������M�͵�P�����ꣻ��������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺��CN��x���ڵ�N��
��A����2��0����B��0��1����C��d��2����
��OA=2��OB=1��CN=2��
�ߡ�CAB=90�㣬����CAN+��BAO=90�㣬
�֡ߡ�CAN+��ACN=90�㣬
���BAO=��ACN��
��Rt��CNA��Rt��AOB��
�� 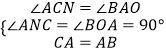 ��
��
��Rt��CNA��Rt��AOB��AAS����
��NC=OA=2��AN=BO=1��
��NO=NA+AO=3���ֵ�C�ڵڶ����ޣ�
��d=��3��
��2��
�⣺�跴��������Ϊy= ![]() ��k��0������C���B���ڸñ�������ͼ���ϣ�
��k��0������C���B���ڸñ�������ͼ���ϣ�
��C�䣨m��2������B�䣨m+3��1����
�ѵ�C���B�������ֱ����y= ![]() ����k=2m��k=m+3��
����k=2m��k=m+3��
��2m=m+3��
��ã�m=3��
��k=6����������������ʽΪy= ![]() ����C�䣨3��2����B�䣨6��1����
����C�䣨3��2����B�䣨6��1����
��ֱ��C��B��Ľ���ʽΪy=ax+b��a��0����
��C�䡢B�������������ã�
![]() ��
��
���ã� 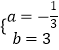 ��
��
��ֱ��C��B��Ľ���ʽΪy=�� ![]() x+3��
x+3��
��3��
�⣺����x���ϵĵ�M�ͷ���������ͼ���ϵĵ�P��ʹ���ı���PGMC����ƽ���ı��Σ�����Ϊ��
��Q��G C����е㣬��y=�� ![]() x+3��x=0���õ�y=3��
x+3��x=0���õ�y=3��
��G��0��3������C�䣨3��2����
��Q�� ![]() ��
�� ![]() ����
����
����Q��ֱ��l��x�ύ��M��㣬��y= ![]() ��ͼ����P��㣬
��ͼ����P��㣬
���ı���P��G M��C����ƽ���ı��Σ�����P��Q=Q M�䣬
��֪��M��ĺ�������� ![]() ����P��ĺ�����С��
����P��ĺ�����С�� ![]() ��
��
��P��H��x���ڵ�H��QK��y���ڵ�K��P��H��QK���ڵ�E����QF��x���ڵ�F��
��QF��P��E��
���M��QF=��QP��E��
�ڡ�P��EQ�͡�QFM���У�
�� 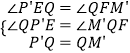 ��
��
���P��EQ�ա�QFM�䣨AAS����
��EQ=FM�䣬P��Q=QM�䣬
��EQ=FM��=t��
���P��ĺ�����x= ![]() ��t����P���������y=2yQ=5����M��������ǣ�
��t����P���������y=2yQ=5����M��������ǣ� ![]() +t��0����
+t��0����
��P���ڷ���������ͼ���ϣ���5�� ![]() ��t��=6��
��t��=6��
��ã�t= ![]() ��
��
��P�䣨 ![]() ��5����M�䣨
��5����M�䣨 ![]() ��0����
��0����
���P��Ϊ����ĵ�P����M��Ϊ����ĵ�M��
����������1����C��CN��ֱ��x�ᣬ��x���ڵ�N����A��B��C������ó�OA��OB��CN�ij����ɡ�CAB=90�㣬����ƽ�Ƕ���õ�һ�Խǻ��࣬��ֱ��������ACN�У���������ǻ��࣬�õ�һ�Խǻ��࣬����ͬ�ǵ������ȵõ�һ�Խ���ȣ�����һ��ֱ����ȣ���AC=BC������AAS��������ACN��������AOBȫ�ȣ�����ȫ�������εĶ�Ӧ����ȿɵó�CN=0A��AN=0B����AN+OA���ON�ij�������C�ڵڶ����ޣ��ɵó�d��ֵ����2���ɵ�һ�������C��B�ĺ�����֮��Ϊ3������ƽ�Ƶ����ʵõ������겻�䣬�����C�䣨m��2������B�䣨m+3��1�����������������������ʽ����C����B����������õ�����k��m�������̣���ȥk�õ�����m�ķ��̣�������̵Ľ�õ�m��ֵ������ȷ����k��ֵ���õ���������������ʽ����ֱ��B��C��Ľ���ʽΪy=ax+b����C����B���������룬�õ�����a��b�Ķ�Ԫһ�η����飬���������Ľ�õ�a��b��ֵ������ȷ����ֱ��B��C��Ľ���ʽ����3������x���ϵĵ�M�ͷ���������ͼ���ϵĵ�P��ʹ���ı���PGMC����ƽ���ı��Σ�����Ϊ����QΪGC����е㣬��ڶ��������ֱ��B��C��Ľ���ʽ��x=0���y��ֵ��ȷ����G�����꣬����C������꣬�����߶��е����깫ʽ���Q�����꣬����Q��ֱ��l��x�ύ��M��㣬��y= ![]() ��ͼ����P��㣬���ı���P��G M��C����ƽ���ı��Σ�����P��Q=Q M�䣬��֪��M��ĺ��������
��ͼ����P��㣬���ı���P��G M��C����ƽ���ı��Σ�����P��Q=Q M�䣬��֪��M��ĺ�������� ![]() ����P��ĺ�����С��
����P��ĺ�����С�� ![]() ����P��H��x���ڵ�H��QK��y���ڵ�K��P��H��QK���ڵ�E����QF��x���ڵ�F������ֱ��ƽ�еõ�һ��ͬλ����ȣ�����һ��ֱ����ȼ�P��Q=QM�䣬����AAS�ɵó���P��EQ���QFM��ȫ�ȣ�����ȫ�������εĶ�Ӧ����ȣ���EQ=FM��=t����Q�ĺ����ꩁt��ʾ��P��ĺ����꣬���뷴������������ʽȷ����P��������꣬����ȷ����M������꣬����P��H��EH=P��H��QF��ʾ��P��E�ij�����P��Q=QM�䣬�ֱ����ֱ���������У����ù��ɶ����г�����t�ķ��̣�������̵Ľ�õ�t��ֵ������ȷ����P����M������꣬��ʱ��P��Ϊ����ĵ�P����M��Ϊ����ĵ�M��
����P��H��x���ڵ�H��QK��y���ڵ�K��P��H��QK���ڵ�E����QF��x���ڵ�F������ֱ��ƽ�еõ�һ��ͬλ����ȣ�����һ��ֱ����ȼ�P��Q=QM�䣬����AAS�ɵó���P��EQ���QFM��ȫ�ȣ�����ȫ�������εĶ�Ӧ����ȣ���EQ=FM��=t����Q�ĺ����ꩁt��ʾ��P��ĺ����꣬���뷴������������ʽȷ����P��������꣬����ȷ����M������꣬����P��H��EH=P��H��QF��ʾ��P��E�ij�����P��Q=QM�䣬�ֱ����ֱ���������У����ù��ɶ����г�����t�ķ��̣�������̵Ľ�õ�t��ֵ������ȷ����P����M������꣬��ʱ��P��Ϊ����ĵ�P����M��Ϊ����ĵ�M��
�����㾫�������ڱ��⿼���ȫ�������ε����ʣ���Ҫ�˽�ȫ�������εĶ�Ӧ�����; ȫ�������εĶ�Ӧ����Ȳ��ܵó���ȷ�𰸣�