题目内容
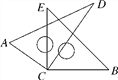
【题目】如图,已知△ABE≌△ACD.
(1)如果BE=6,DE=2,求BC的长;
(2)如果∠BAC=75°,∠BAD=30°,求∠DAE的度数.

【答案】(1)10;(2)15°
【解析】
(1)根据全等三角形的性质,可得出BE=CD,根据BE=6,DE=2,得出CE=4,从而得出BC的长;
(2)根据全等三角形的性质可得出∠BAE=∠CAD,即可得出∠BAD=∠CAE,计算∠CAD﹣∠CAE即得出答案.
解:(1)∵△ABE≌△ACD,
∴BE=CD,∠BAE=∠CAD,
又∵BE=6,DE=2,
∴EC=DC﹣DE=BE﹣DE=4,
∴BC=BE+EC=10;
(2)∠CAD=∠BAC﹣∠BAD=75°﹣30°=45°,
∴∠BAE=∠CAD=45°,
∴∠DAE=∠BAE﹣∠BAD=45°﹣30°=15°.

练习册系列答案
相关题目