题目内容
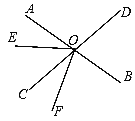
【题目】如图,直线AB、CD相交于点O.已知∠BOD=75°,OE把∠AOC分成两个角,且∠AOE:∠EOC=2:3.
(1)求∠AOE的度数;
(2)若OF平分∠BOE,问:OB是∠DOF的平分线吗?试说明理由.
【答案】(1) 30°;(2) OB是∠DOF的平分线,理由见解析
【解析】
(1)设∠AOE=2x,根据对顶角相等求出∠AOC的度数,根据题意列出方程,解方程即可;
(2)根据角平分线的定义求出∠BOF的度数即可.
(1)∵∠AOE:∠EOC=2:3.∴设∠AOE=2x,则∠EOC=3x,∴∠AOC=5x.
∵∠AOC=∠BOD=75°,∴5x=75°,解得:x=15°,则2x=30°,∴∠AOE=30°;
(2)OB是∠DOF的平分线.理由如下:
∵∠AOE=30°,∴∠BOE=180°﹣∠AOE=150°.
∵OF平分∠BOE,∴∠BOF=75°.
∵∠BOD=75°,∴∠BOD=∠BOF,∴OB是∠DOF的角平分线.

练习册系列答案
相关题目