题目内容
【题目】如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点E.
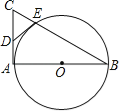
(1)若D为AC的中点,证明DE是⊙O的切线;
(2)若OA=![]() ,CE=1,求△ABC的面积.
,CE=1,求△ABC的面积.
【答案】(1)见解析;(2)2![]()
【解析】试题分析:(1)连接AE,OE,∠AEB=90°,∠BAC=90°,在Rt△ACE中,D为AC的中点,则DE=AD=CD=![]() AC,得出∠DEA=∠DAE,由OA=OE,得出∠OAE=∠OEA,则∠DEO=∠DEA+∠OEA=∠DAE+∠OAE=∠BAC=90°,即可得出结论;
AC,得出∠DEA=∠DAE,由OA=OE,得出∠OAE=∠OEA,则∠DEO=∠DEA+∠OEA=∠DAE+∠OAE=∠BAC=90°,即可得出结论;
(2)AB=2AO=2![]() ,由△BCA∽△BAE,得出
,由△BCA∽△BAE,得出![]() =
=![]() ,求出BE=3,BC=4,由勾股定理得AC=
,求出BE=3,BC=4,由勾股定理得AC=![]() =2,则S△ABC=
=2,则S△ABC=![]() ABAC代入即可得出结果.
ABAC代入即可得出结果.
(1)证明:连接AE,OE,如图所示:
∵AB是⊙O的直径,
∴∠AEB=90°,
∵AC是⊙O的切线,
∴∠BAC=90°,
∵在Rt△ACE中,D为AC的中点,
∴DE=AD=CD=![]() AC,
AC,
∴∠DEA=∠DAE,
∵OA=OE,
∴∠OAE=∠OEA,
∴∠DEO=∠DEA+∠OEA=∠DAE+∠OAE=∠BAC=90°,
∴OE⊥DE,
∵OE为半径,
∴DE是⊙O的切线;
(2)解:∵AO=![]() ,
,
∴AB=2AO=2![]() ,
,
∵∠CAB=∠AEB=90°,∠B=∠B,
∴△BCA∽△BAE,
∴![]() =
=![]() ,即AB2=BEBC=BE(BE+EC),
,即AB2=BEBC=BE(BE+EC),
∴(2![]() )2=BE2+BE,
)2=BE2+BE,
解得:BE=3或BE=﹣4(不合题意,舍去),
∴BE=3,
∴BC=BE+CE=3+1=4,
∴在Rt△ABC中,AC=![]() =
=![]() =2,
=2,
∴S△ABC=![]() ABAC=
ABAC=![]() ×2
×2![]() ×2=2
×2=2![]() .
.


练习册系列答案
相关题目