题目内容
【题目】已知抛物线G1:y=ax2+bx+c的顶点为(2,﹣3),且经过点(4,1).
(1)求抛物线G1的解析式;
(2)将抛物线G1先向左平移3个单位,再向下平移1个单位后得到抛物线G2,且抛物线G2与x轴的负半轴相交于A点,求A点的坐标;
(3)如果直线m的解析式为![]() ,点B是(2)中抛物线G2上的一个点,且在对称轴右侧部分(含顶点)上运动,直线n过点A和点B.问:是否存在点B,使直线m、n、x轴围成的三角形和直线m、n、y轴围成的三角形相似?若存在,求出点B的坐标;若不存在,请说明理由.
,点B是(2)中抛物线G2上的一个点,且在对称轴右侧部分(含顶点)上运动,直线n过点A和点B.问:是否存在点B,使直线m、n、x轴围成的三角形和直线m、n、y轴围成的三角形相似?若存在,求出点B的坐标;若不存在,请说明理由.
【答案】(1):y=(x﹣2)2﹣3=x2﹣4x+1,(2)A(﹣3,0).(3)见解析
【解析】
试题分析:(1)先设为顶点式,再把顶点坐标和经过的点(4,1)代入即可解决,
(2)根据平移规则直接写出抛物线G2的解析式,令y=0,即可求出点A的坐标,
(3)分为交点咋x轴上方,与下方进行分析,根据相似确定角的大小,进一步得到直线n的斜率,求出与y轴的交点坐标,由点A(﹣3,0),运用待定系数法,确定直线n的解析式,联立抛物线G2,解方程组即可求解.
解:由抛物线G1:y=ax2+bx+c的顶点为(2,﹣3),且经过点(4,1),
可设抛物线G1:y=a(x﹣2)2﹣3,
把(4,1)代入得:1=4a﹣3,解得:a=1,
所以抛物线G1:y=(x﹣2)2﹣3=x2﹣4x+1,
(2)抛物线G1:y=(x﹣2)2﹣3先向左平移3个单位,再向下平移1个单位后得到抛物线G2:y=(x+1)2﹣4,
令y=0,得:0=(x+1)2﹣4,解得:x=﹣3,或x=1(舍去),
所以点A(﹣3,0).
(3)直线m与x轴,y轴的交点分别为F,E,
当直线n与G2交点在x轴上方时,直线n与x轴,y轴的交点为A,D,与抛物线交点B,与直线m交与点C,
当直线n与G2交点在x轴下方时,直线n1与x轴,y轴的交点为A,H,与抛物线交点B1,与直线m交与点L,
当直线n与G2交点在x轴上方时,如图1:
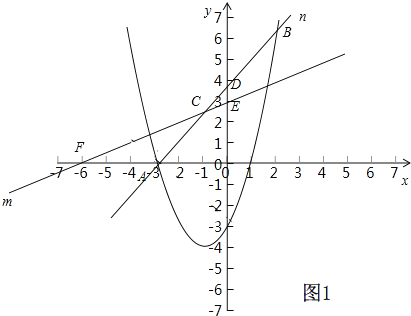
由题意△CDE∽△CFA,此时有:∠CDE=∠CFA,
直线m的解析式为![]() ,当x=0时,y=3,当y=0时,x=﹣6,
,当x=0时,y=3,当y=0时,x=﹣6,
∴点E(0,3),点F(﹣6,0),
∴OF=6,OE=3,
∴tan∠CDE=tan∠CFA=![]() ,
,
∴![]() =
=![]() ,
,
∵OA=3,
∴OD=6,
点D(0,6),
设直线n:y=mx+n,把D(0,6),点A(﹣3,0)代入得:![]() ,
,
解得:![]() ,
,
∴直线n:y=2x+6,
联立直线n和抛物线G2得:![]() ,
,
解得:x=3,或x=﹣3(舍去)
此时y=12,
所以:点B(3,12),
当直线n与G2交点在x轴下方时,如图2:
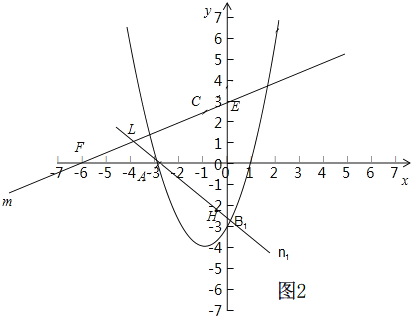
由题意△HLE∽△FLA,此时有:∠ELH=∠FLA=90°,
∠EHA=∠LFA,
直线m的解析式为![]() ,当x=0时,y=3,当y=0时,x=﹣6,
,当x=0时,y=3,当y=0时,x=﹣6,
∴点E(0,3),点F(﹣6,0),
∴OF=6,OE=3,
∴tan∠EHA=tan∠LFA=![]() ,
,
∴![]() =
=![]() ,
,
∵OA=3,
∴OH=6,
点H(0,﹣6),
设直线n:y=mx+n,把D(0,﹣6),点A(﹣3,0)代入得:![]()
解得:![]() ,
,
∴直线n:y=﹣2x﹣6,
联立直线n和抛物线G2得: ,
,
解得:x=﹣1,或x=﹣3(舍去)
此时y=﹣4,
所以:点B1(﹣1,﹣4),
综上所述:存在点B,使直线m、n、x轴围成的三角形和直线m、n、y轴围成的三角形相似,点B的坐标为(3,12)和(﹣1,﹣4).

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案