题目内容
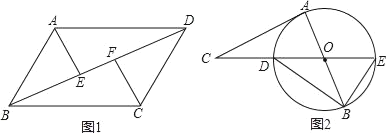
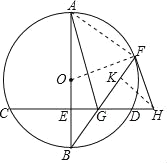
【题目】如图,AB是⊙O的直径,CD是⊙O的弦,且AB⊥CD于E,F为![]() 上一点,BF交CD于G,点H在CD的延长线上,且FH=GH.
上一点,BF交CD于G,点H在CD的延长线上,且FH=GH.

(1)求证:FH与⊙O相切.
(2)若FH=OA=5,FG=3![]() ,求AG的长.
,求AG的长.
【答案】(1)见解析;(2)6
【解析】
(1)连接OF,通过角之间的等量代换证明∠OFH为90°,即可得FH与⊙O相切;
(2)连接AF,作HK⊥FG于K,由FH=GH,利用等腰三角形的三线合一,可求KG,进而得出sin∠EBG等于sin∠KHG,求出AF,在直角三角形AFG中,利用勾股定理可求得AG的长.
(1)证明:连接OF,
∵FH=GH.
∴∠GFH=∠FGH,
∵∠FGH=∠BGE,
∴∠GFH=∠BGE,
∵OB=OF,
∴∠B=∠BFO,
∵AB⊥CD,
∴∠B+∠BGE=90°,
∴∠BFO+∠GFH=90°,即∠OFH=90°,
∴FH与⊙O相切;
(2)解:连接AF,作HK⊥FG于K,
∵HF=HG,HK⊥FG,
∴FK=KG=![]() ,
,
∵HF=HG,FH=OA=5,
∴HF=HG=5,
∵∠BEG=∠HKG=90°,∠BGE=∠HGK,
∴∠EBG=∠KHG,
∵AB为⊙O的直径,
∴∠AFB=90°,
∴sin∠EBG=sin∠KHG=![]() ÷5=
÷5=![]() ,
,
∴AF=![]() ,
,
∴在直角三角形AFG中,AG=![]() =6.
=6.
∴AG的长为6.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目