题目内容
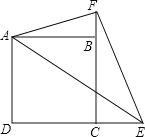
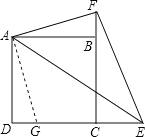
【题目】正方形ABCD中,点E在DC延长线上,点F在CB延长线上,∠EAF=45°,∠BAF=15°
(1)求证:DE﹣EF=BF;
(2)若AD=![]() ,求△AEF的面积.
,求△AEF的面积.
【答案】(1)证明见解析;(2)3![]() ﹣3.
﹣3.
【解析】
试题
(1)在DE上取一点G,使DG=BF,先证:△ABF≌△ADG;再证:△AFE≌△AGE可得EF=GE,从而可得DE-EF=DE-GE=DG=BF;
(2)由AB∥CD,可得∠AED=∠BAE=30°,从而可在△ADE中求得DE=3,进而可得CE=3﹣![]() ;再由(1)△AFE≌△AGE可得∠AEF=∠AED=30°,进而可得∠CFE=90°﹣∠AEF﹣∠AED=90°﹣30°﹣30°=30°,从而可得:GE=EF=2CE=2(3﹣
;再由(1)△AFE≌△AGE可得∠AEF=∠AED=30°,进而可得∠CFE=90°﹣∠AEF﹣∠AED=90°﹣30°﹣30°=30°,从而可得:GE=EF=2CE=2(3﹣![]() )=6﹣
)=6﹣![]() ,由S△AEF=S△AGE=
,由S△AEF=S△AGE=![]() GE
GE![]() AD就可计算出所求面积.
AD就可计算出所求面积.
试题解析:
(1)在DE上取一点G,使DG=BF,
∵四边形ABCD是正方形,
∴AD=AB,∠D=∠ABC=∠ABF=90°,
在△ABF和△ADG中,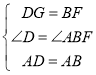 ,
,
∴△ABF≌△ADG(SAS),
∴∠DAG=∠BAF=15°,AG=AF,
∵∠EAF=45°,∠BAF=15°,
∴∠BAE=∠EAF﹣∠BAF=45°﹣15°=30°,
∴∠GAE=90°﹣15°﹣30°=45°,
∴∠GAE=∠FAE=45°,
在△AFE和△AGE中,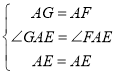 ,
,
∴△AFE≌△AGE(SAS),
∴EF=GE,
∴EF+BF=EG+DG=DE,
∴DE﹣EF=BF;
(2)∵AB∥CD,
∴∠AED=∠BAE=30°,
∴DE=![]() AD=
AD=![]() ×
×![]() =3,
=3,
∴CE=DE﹣CD=3﹣![]() ,
,
由(1)△AFE≌△AGE可得∴∠AEF=∠AED=30°,
∴∠CFE=90°﹣∠AEF﹣∠AED=90°﹣30°﹣30°=30°,
∴GE=EF=2CE=2(3﹣![]() )=6﹣2
)=6﹣2![]() ,
,
∴S△AGE=![]() (6﹣2
(6﹣2![]() )×
)×![]() =3
=3![]() ﹣3,
﹣3,
∴S△AEF=S△AGE=3![]() ﹣3.
﹣3.

 名校课堂系列答案
名校课堂系列答案