题目内容
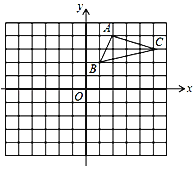
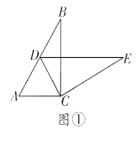
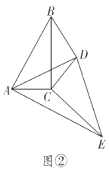
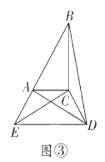
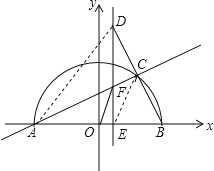
【题目】如图,在平面直角坐标系中,点A(-5,0),以OA为半径作半圆,点C是第一象限内圆周上一动点,连结AC、BC,并延长BC至点D,使CD=BC,过点D作x轴垂线,分别交x轴、直线AC于点E、F,点E为垂足,连结OF.
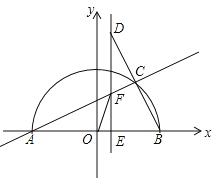
(1)当∠BAC=30时,求△ABC的面积;
(2)当DE=8时,求线段EF的长;
(3)在点C运动过程中,是否存在以点E、O、F为顶点的三角形与△ABC相似,若存在,请求出点E的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)3;(3)存在,点E的坐标为(
;(2)3;(3)存在,点E的坐标为(![]() ,0) ;(
,0) ;(![]() ,0);(
,0);(![]() ,0)
,0)
【解析】
(1)根据圆周角定理求得∠ACB=90°,根据30°的直角三角形的性质求得BC,进而根据勾股定理求得AC,然后根据三角形面积公式即可求得;
(2)连接AD,由垂直平分线的性质得AD=AB=10,又DE=8,在Rt△ODE中,由勾股定理求AE,依题意证明△AEF∽△DEB,利用相似比求EF;
(3)当以点E、O、F为顶点的三角形与△ABC相似时,分为两种情况:①当交点E在O,B之间时;②当点E在O点的左侧时;分别求E点坐标.
(1)∵AB是⊙O的直径,
∴∠ACB=90°,
在Rt△ABC中,AB=10,∠BAC=30°,
∴BC=![]() AB=5,
AB=5,
∴AC=![]() ,
,
∴S△ABC=![]() ACBC=
ACBC=![]() ;
;
(2)连接AD,
∵∠ACB=90°,CD=BC,
∴AD=AB=10,
∵DE⊥AB,
∴AE=![]() =6,
=6,
∴BE=ABAE=4,
∴DE=2BE,
∵∠AFE+∠FAE=90°, ∠DBE+∠FAE=90°,
∴∠AFE=∠DBE,
∵∠AEF=∠DEB=90°,
∴△AEF∽△DEB,
∴![]() =2,
=2,
∴EF=![]() AE=
AE=![]() ×6=3;
×6=3;
(3)连接EC,设E(x,0),
当![]() 的度数为60°时,点E恰好与原点O重合;
的度数为60°时,点E恰好与原点O重合;
①0°<![]() 的度数<60°时,点E在O、B之间,∠EOF>∠BAC=∠D,
的度数<60°时,点E在O、B之间,∠EOF>∠BAC=∠D,
又∵∠OEF=∠ACB=90°,由相似知∠EOF=∠EBD,此时有△EOF∽△EBD,
∴![]() ,
,
∵EC是Rt△BDE斜边的中线,
∴CE=CB,
∴∠CEB=∠CBE,
∴∠EOF=∠CEB,
∴OF∥CE,
∴△AOF∽△AEC
∴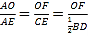 ,∴
,∴![]() ,即
,即![]() ,
,
解得x=![]() ,因为x>0,
,因为x>0,
∴x=![]() ;
;
②60°<![]() 的度数<90°时,点E在O点的左侧,
的度数<90°时,点E在O点的左侧,
若∠EOF=∠B,则OF∥BD,
∴OF=![]() BC=
BC=![]() BD,
BD,
∴![]() 即
即![]() 解得x=
解得x=![]() ,
,
若∠EOF=∠BAC,则x=![]() ,
,
综上点E的坐标为(![]() ,0) ;(
,0) ;(![]() ,0);(
,0);(![]() ,0).
,0).

 备战中考寒假系列答案
备战中考寒假系列答案【题目】今年4月份,某校九年级学生参加了广州市中考体育考试,为了了解该校九年级(1)班同学的中考体育情况,对全班学生的中考体育成绩进行了统计,并绘制以下不完整的频数分布表(如表)和扇形统计图(如图),根据图表中的信息解答下列问题:
分组 | 分数段(分) | 频数 |
|
| 2 |
|
| 5 |
|
| 15 |
|
|
|
|
| 10 |
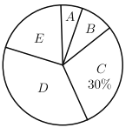
(1)求全班学生人数和![]() 的值.
的值.
(2)直接写出该班学生的中考体育成绩的中位数落在哪个分数段.
(3