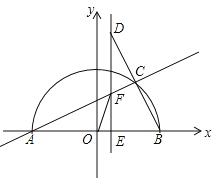题目内容
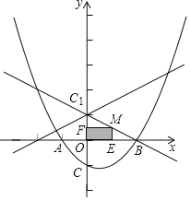
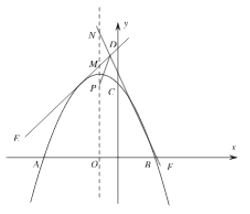
【题目】已知抛物线y=ax2-x+c的对称轴为直线x=-1,与x轴交于点A(-4,0)和点B,与y轴交于点C,点D(m,n)为坐标轴中一点,点O为坐标原点.
(1)求抛物线的解析式;
(2)若m=0,∠DAB=∠BCO,射线AD与抛物线交于点H,请画出图形,求出点H的坐标;
(3)若n=5,m≠-1,直线DE和DF(不与x轴垂直)都与抛物线只有一个公共点,DE和DF分别与对称轴交于点M,N,点P为对称轴上(M,N下方)一点,当PD2=PMPN时,请画出图形,求出点P的坐标.
【答案】(1)![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() 或
或![]() ;(3)点
;(3)点![]() 的坐标为
的坐标为![]() .
.
【解析】
(1)由抛物线的对称轴为直线![]() ,得出
,得出![]() ,再将
,再将![]() 代入解得
代入解得![]() ,即可得到解析式;
,即可得到解析式;
(2)当![]() 时,求出抛物线与x轴交点
时,求出抛物线与x轴交点![]() ,
,![]() ,当
,当![]() 时,得到C(0,4),可得AO=CO=4,OB=2,因为
时,得到C(0,4),可得AO=CO=4,OB=2,因为![]() ,所以点
,所以点![]() 在
在![]() 轴上,分成两种情况讨论,①当
轴上,分成两种情况讨论,①当![]() 在
在![]() 轴正半轴上时,通过证明
轴正半轴上时,通过证明![]() ,得到OB=OD,即点D为(0,2),求出直线AD的解析式,联立直线AD的解析式和抛物线的解析式,得到点H的坐标;②当点
,得到OB=OD,即点D为(0,2),求出直线AD的解析式,联立直线AD的解析式和抛物线的解析式,得到点H的坐标;②当点![]() 在
在![]() 轴负半轴上时,通过证明
轴负半轴上时,通过证明![]() ,得到OB=OD,即点D为(0,-2),求出直线AD的解析式,联立直线AD的解析式和抛物线的解析式,得到点H的坐标即可;
,得到OB=OD,即点D为(0,-2),求出直线AD的解析式,联立直线AD的解析式和抛物线的解析式,得到点H的坐标即可;
(3)设经过点![]() 的直线解析式为
的直线解析式为![]() ,将
,将![]() 代入,得到
代入,得到![]() ,所以经过点
,所以经过点![]() 的直线解析式可以表示为
的直线解析式可以表示为![]() ,联立过点D的解析式和抛物线的解析式得到
,联立过点D的解析式和抛物线的解析式得到![]() ,因为经过点
,因为经过点![]() 的直线
的直线![]() 和
和![]() 都与抛物线只有一个交点,得到
都与抛物线只有一个交点,得到![]() ,设直线
,设直线![]() 的解析式为
的解析式为![]() ,直线DF的解析式为
,直线DF的解析式为![]() ,可得
,可得![]() ,
,![]() ,在
,在![]() 中,当
中,当![]() 时,
时,![]() ,得到
,得到![]() ;在
;在![]() 中,当
中,当![]() 时,
时,![]() ,得到
,得到![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,
,![]() ,因为
,因为![]() ,列出方程,解得t=4,即可得到点
,列出方程,解得t=4,即可得到点![]() 的坐标;
的坐标;
解:(1)∵抛物线的对称轴为直线![]() ,
,
![]() ,
,
![]() ,
,
![]() ,将
,将![]() 代入解得
代入解得![]() ,
,
![]() 抛物线的解析式为:
抛物线的解析式为:![]() ;
;
(2)当![]() 时,
时,![]() 解得
解得![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,
![]() ,
,![]() ,
,
∵![]() ,
,
![]() 点
点![]() 在
在![]() 轴上,
轴上,
①当点![]() 在
在![]() 轴正半轴上时,如图所示,
轴正半轴上时,如图所示,
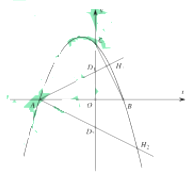
∵![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
设![]() 的解析式为
的解析式为![]() ,将
,将![]() ,
,![]() 代入解得
代入解得![]() ,
,
联立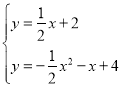 ,
,
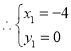 ,
,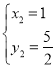 ,
,
![]() ,
,
②当点![]() 在
在![]() 轴负半轴上时,如图所示,
轴负半轴上时,如图所示,
∵![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
设![]() 的解析式为
的解析式为![]() ,将
,将![]() ,
,![]() 代入解得
代入解得![]() ,
,
联立![]() ,
,
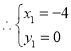 ,
,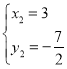 ,
,
![]() ,
,
综上所述:点![]() 的坐标为
的坐标为![]() 或
或![]() ,
,
(3)设经过点![]() 的直线解析式为
的直线解析式为![]() ,将
,将![]() 代入,
代入,
![]() ,
,
![]() ,
,
![]() 经过点
经过点![]() 的直线解析式可以表示为
的直线解析式可以表示为![]() ,
,
联立 ,
,
![]() ,
,
∵经过点![]() 的直线
的直线![]() 和
和![]() 都与抛物线只有一个交点,
都与抛物线只有一个交点,
![]() ,
,
![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,
,
直线DF的解析式为![]() ,
,
则![]() ,
,![]() ,
,
在![]() 中,当
中,当![]() 时,
时,![]() ,
,
![]() ,
,
在![]() 中,当
中,当![]() 时,
时,![]() ,
,
![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
![]() ,
,
![]()
∵![]() ,
,
![]() ,
,
![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ;
;

 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案