题目内容
【题目】在![]() 中,
中,![]() ,点
,点![]() 分别是边
分别是边![]() 的中点,连接
的中点,连接![]() ,
,
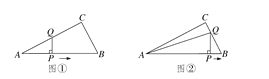
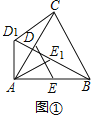
(1)如图①,当![]() 时,
时,![]() 绕点
绕点![]() 逆时针旋转得到
逆时针旋转得到![]() ,连接
,连接![]() 、
、![]() ,
,![]() 在旋转过程中请猜想:
在旋转过程中请猜想:![]() ______(直接写出答案);
______(直接写出答案);
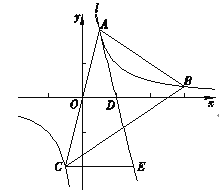
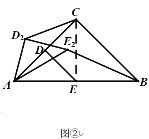
(2)如图②,当![]() 时,
时,![]() 绕点
绕点![]() 逆时针旋转得到
逆时针旋转得到![]() ,连接
,连接![]() 、
、![]() ,
,![]() 在旋转过程中请猜想:
在旋转过程中请猜想:![]() 的比值,并证明你的猜想;
的比值,并证明你的猜想;
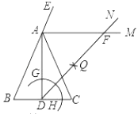
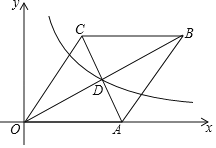
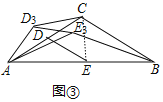
(3)如图③,当![]() 时,
时,![]() 绕点
绕点![]() 逆时针旋转得到
逆时针旋转得到![]() ,连接
,连接![]() 、
、![]() ,请直接写出
,请直接写出![]() 在旋转过程中
在旋转过程中![]() 的比值.(用含
的比值.(用含![]() 的代数式表示)
的代数式表示)
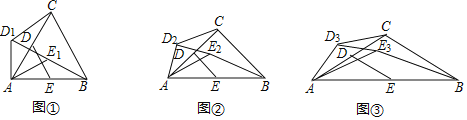
【答案】(1)1;(2)![]() ;理由见解析;(3)
;理由见解析;(3)![]() 的比值是定值,
的比值是定值,![]() ,理由见解析.
,理由见解析.
【解析】
(1)如图①中,利用等边三角形的性质证明![]() 即可.
即可.
(2)结论:![]() ,证明
,证明![]() 即可解决问题.
即可解决问题.
(3)结论:![]() 的比值是定值,
的比值是定值,![]() 证明方法类似(2).
证明方法类似(2).
解:(1)如图①中, ∵CA=CB,∠CAB=60°,
∴△ACB是等边三角形,
![]() 点
点![]() 分别是边
分别是边![]() 的中点,
的中点,
![]() AD=DC,AE=EB,
AD=DC,AE=EB,
∴△AED,![]() 都是等边三角形,
都是等边三角形,
∴![]() AC=AB,
AC=AB,
∴![]()
∴![]() (SAS),
(SAS),
∴![]() ,
,
∴![]()
故答案为1.
(2)![]()
理由:如图②中,连接![]()
∵![]() ,点
,点![]() 是边
是边![]() 的中点,
的中点,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 中,
中,
∵![]() ,
,![]() ,
,
∴![]()
![]()
![]()
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3)![]() 的比值是定值,
的比值是定值,![]() .
.
理由:如图③中,连接EC.
∵CA=CB,AE=EB,
∴CE⊥AB,
∴![]()
同法可证:![]()
∴![]()
![]()
![]() 的比值是定值,
的比值是定值,![]() .
.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目