题目内容
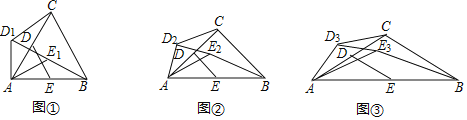
【题目】如图，平行四边形
，点
是
上的一点，连结
，
，
平分
，交
于点
，且点是的中点，连结
，已知
，
，则
________．
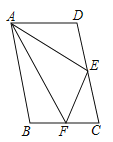
【答案】4
【解析】
如下图，延长AE与BC，交于点G，先证△ADE≌△GCE，得到CG=AD=5，再利用角度转化，得出△AFG是等腰三角形，最后在等腰△AFG中求得FE的长．
如下图，延长AE与BC，交于点G
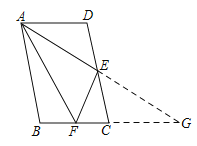
∵四边形ABCD是平行四边形，∴AD∥BC
∴∠DAE=∠CGE，∠ADE=∠GCE
∵点E是DC的中点，∴DE=EC
∴△ADE≌△GCE(AAS)
∴CG=AD=5，AE=EG
∵CF=3，∴FG=8
∵∠FAD=60°，AE是∠FAD的角平分线
∴∠FAE=∠EAD=30°，∴∠CGE=∠EAD=30°
∴∠FAE=∠FGE，△FAG是等腰三角形
∴AF=FG=8
∵AE=EG，△FAG是等腰三角形
∴EF⊥AG
∴△AEF是直角三角形，且AF=8，∠FAE=30°
∴EF=4
故答案为：4
练习册系列答案
相关题目
