Question

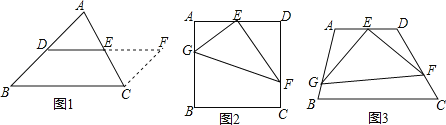
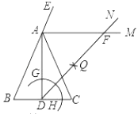
【题目】如图，在△ABC中，AB＝AC=6，BC=4，AD是BC边上的高，AM是△ABC外角∠CAE的平分线．以点D为圆心，适当长为半径画弧，交DA于点G，交DC于点H．再分别以点G、H为圆心，大于GH的长为半径画弧，两弧在∠ADC内部交于点Q，连接DQ并延长与AM交于点F，则DF的长度为（ ）．

A.6B.C.D.8

Answer 1

【答案】D

【解析】

根据画图过程可得：DF平分∠ADC，∠ADF=∠CDF，根据AB=AC，得∠B=∠ACB，由AM是△ABC外角∠CAE的平分线，证得∠EAF=∠B，得AF∥BC，进而证明△ADF为等腰直角三角形，即可求出DF的长

解:根据画图过程可知:DF平分∠ADC,

∴∠ADF=∠CDF,

∵AB=AC,

∴∠B=∠ACB,

∵AM是△A BC外角∠CAE的平分线,

∴∠EAM=∠CAM,

∵∠EAC=∠B+∠ACB,

∴∠EAF=∠B,

∵AF//BC,

∴∠AFD=∠FDC, ∠FAD=∠ADB

∴∠AFD=∠ADF,

∴AF=AD,

∵AD是高， AB＝AC=6，BC=4，

∴∠ADB=90°, ,

∴∠FAD=∠ADB=90°

∴ ,

∵AF=AD , ∠FAD=90°

∴△ADF的形状是等腰直角三角形．

∴DF=

故选: D．