Question

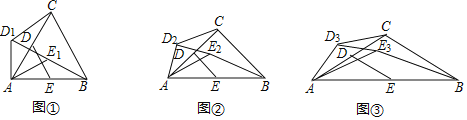
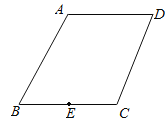
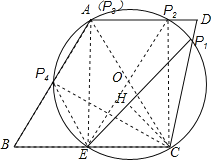
【题目】已知：如图，四边形ABCD中，AD∥BC，AB＝BC＝4，∠B＝60°，∠C＝105°，点E为BC的中点，以CE为弦作圆，设该圆与四边形ABCD的一边的交点为P，若∠CPE＝30°，则EP的长为_____．

Answer 1

【答案】或4或2或2

【解析】

如图，连接AC，AE，根据已知条件得到△ABC是等边三角形，求得BE=CE=2，AE⊥BC，∠EAC=30°，推出AC是以CE为弦的圆的直径，设圆心为O，当⊙O与CD边交于，则，过C作于H，解直角三角形得到；当⊙O与AD交于，A()，由AD∥CE，推出四边形是矩形，得到，P3E=CE=2，当⊙O与AB交于，得到是等边三角形，求得，于是得到结论．

如图，连接AC，AE，

∵AB=BC=4，∠B=60°，

∴△ABC是等边三角形，

∵点E为BC的中点，

∴BE=CE=2，AE⊥BC，∠EAC=30°，

∴AC是以CE为弦的圆的直径，

设圆心为O，

当⊙O与CD边交于P1，则∠EP1C=∠EAC=30°，

∵∠ECP1=105°，

∴∠P1EC=45°，

过C作CH⊥P1E于H，

∴EH=CH=CE=，

∴P1H=HC=，

∴；

当⊙O与AD交于P2、A(P3)，

∵AD∥CE，

∴∠ECP2=∠AP2C=90°，

∴四边形AECP2是矩形，

∴P2E=AC=4，P3E=CE=2，

当⊙O与AB交于P4，

∵∠AP4C=90°，∠EP4C=30°，

∴∠BP4E=60°，

∴△BP4E是等边三角形，

∴P4E=BE=2，

综上所述，若∠CPE=30°，则EP的长为或4或2或2，

故答案为：或4或2或2．