题目内容
【题目】如图,在直角坐标系![]() 中,
中,![]() ,
,![]() ,
,![]() 是线段
是线段![]() 上靠近点
上靠近点![]() 的三等分点.
的三等分点.

(1)若点![]() 是
是![]() 轴上的一动点,连接
轴上的一动点,连接![]() 、
、![]() ,当
,当![]() 的值最小时,求出点
的值最小时,求出点![]() 的坐标及
的坐标及![]() 的最小值;
的最小值;
(2)如图2,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,再将
,再将![]() 绕点
绕点![]() 作顺时针方向旋转,旋转角度为
作顺时针方向旋转,旋转角度为![]() ,记旋转中的三角形为
,记旋转中的三角形为![]() ,在旋转过程中,直线
,在旋转过程中,直线![]() 与直线
与直线![]() 的交点为
的交点为![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,当
,当![]() 为等腰三角形时,请直接写出
为等腰三角形时,请直接写出![]() 的值.
的值.
【答案】(1)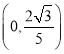 ,
,![]() ;(2)α的值为45°,90°,135°,180°.
;(2)α的值为45°,90°,135°,180°.
【解析】
(1)作HG⊥OB于H.由HG∥AO,求出OG,HG,即可得到点H的坐标,作点B关于y轴的对称点B′,连接B′H交y轴于点M,则B'(-2,0),此时MB+MH的值最小,最小值等于B'H的长;求得直线B′H的解析式为y=![]() ,即可得到点M的坐标为
,即可得到点M的坐标为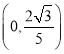 .
.
(2)依据△OST为等腰三角形,分4种情况画出图形,即可得到旋转角的度数.
解:(1)如图1,作HG⊥OB于H.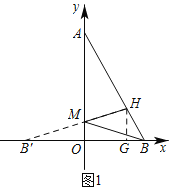
∵HG∥AO,
∴![]()
∵OB=2,OA=![]() ,
,
∴GB=![]() ,HG=
,HG=![]() ,
,
∴OG=OB-GB=![]() ,
,
∴H(![]() ,
,![]() )
)
作点B关于y轴的对称点B′,连接B′H交y轴于点M,则B'(-2,0),
此时MB+MH的值最小,最小值等于B'H的长.
∵B'(-2,0),H(![]() ,
,![]() )
)
![]() B'H=
B'H=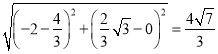
∴MB+MH的最小值为![]()
设直线B'H的解析式为y=kx+b,则有
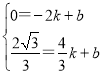
解得: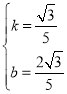
∴直线B′H的解析式为
当x=0时,y=![]()
∴点M的坐标为: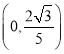
(2)如图,当OT=OS时,α=75°-30°=45°;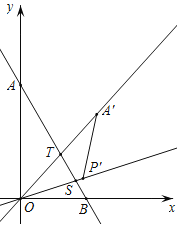
如图,当OT=TS时,α=90°;
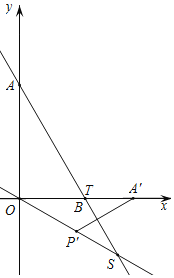
如图,当OT=OS时,α=90°+60°-15°=135°;
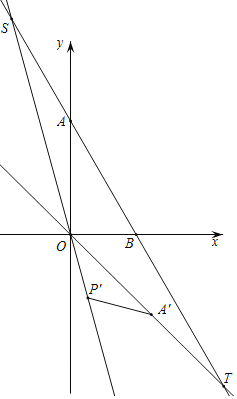
如图,当ST=OS时,α=180°;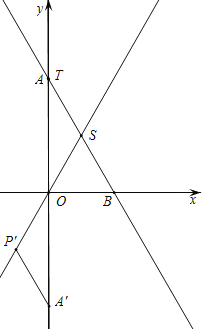
综上所述,α的值为45°,90°,135°,180°.

练习册系列答案
相关题目