Question

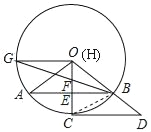
【题目】△OAB是⊙O的内接三角形，∠AOB=120°，过O作OE⊥AB于点E，交⊙O于点C，延长OB至点D，使OB=BD，连CD．

（1）求证： CD是⊙O切线；

（2）若F为OE上一点，BF的延长线交⊙O于G，连OG，，CD=6，求S△GOB．

Answer 1

【答案】(1)详见解析；（2）9.

【解析】试题分析：（1）证明BC=OB=BD，可得∠OCD=90°，所以CD是⊙O切线；

（2）先求BE=3，⊙O的半径为6，过G作GH⊥OE于H，求GH的长也是6，即H与O重合，OG⊥OF，根据比例=，求得OF=12-6，最后利用面积和求面积．

试题解析：（1）连接BC，

∵OA=OB，OE⊥AB，

∴∠AOC=∠BOC，

∵∠AOB=120°，

∴∠AOC=∠BOC=60°，

∵OC=OB，

∴BC=OB=BD，

∴CB=OD，

∴∠OCD=90°，

∴CD是⊙O切线；

（2）由（1）知：∠OCD=90°，

∵∠OEB=90°，

∴AB∥CD，

∴△OEB∽△OCD，

∴，

∴，

∴BE=3，

Rt△OEB中，sin60°=，

∴OB=3 =6，

∴OC=6，OE=3，

过G作GH⊥OE于H，

∴GH∥BE，

∴△GHF∽△BEF，

∴，

∴，

∴GH=6，

∴GH=OG=6，

即H与O重合，OG⊥OF，

∴，

∵OF+EF=OE=3，

∴OF=12﹣6，

∴S△GOB=S△GOF+S△BOF=OG=（OG+BE）=（12﹣6）（6+3）=9．