题目内容
【题目】在 Rt△ABC 中,∠BAC=90°,AC=AB,点 F 是射线 CA 上一点,连接 BF,过 C 作 CE⊥BF,垂足为点 E,直线 CE,AB 相交于点 D.
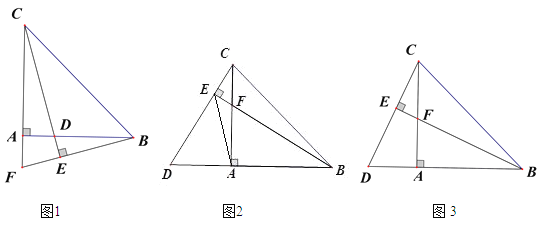
(1)如图 1,当点 F 在线段 CA 延长线上时,求证:AB+AD=CF;
(2)如图 2,当点 F 在线段 CA 上时,连接 EA,求证:EA 平分∠DEB;
(3)如图 3,当点 F 恰好为线段 CA 的中点时,EF=1,试求△BDE 的面积.
【答案】(1)证明见解析;(2) 证明见解析;(3)9
【解析】
(1)根据题意可以得到△ACD≌△ABF,然后根据全等三角形的性质可以证明结论成立.
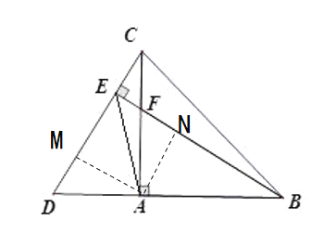
(2)过A作AM⊥CD于M, 作AN⊥BE于N可证Rt△CAM≌Rt△BAN,得到AM=AN,利用角平分线的判定即可证明;
(3)可证△CAD≌△BAF,设AD=AF=x则CF=AF=x, ![]() ,AB=AC=2x,由∠DCA=∠FCE,∠DAC=∠CEF=90°.可得
,AB=AC=2x,由∠DCA=∠FCE,∠DAC=∠CEF=90°.可得![]() 根据
根据![]() 列出方程
列出方程![]() 求出x的值,求出DE、BE的长即可得出答案.
求出x的值,求出DE、BE的长即可得出答案.
(1)证明:∵∠BAC=90°,
∴∠CAD=∠FAB=90°.
∵CE⊥BF
∴∠DEB=90°.
∵∠ADC=∠EDB.
∴∠ACD=∠DBE
在Rt△CAD和Rt△BAF中,
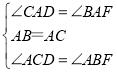 ,
,
∴Rt△CAD≌Rt△BAF,
∴AF=AD
∵AC+AF=CF
∴AB+AD=CF
(2)过A作AM⊥CD于M, 作AN⊥BE于N
∴∠CMA=∠BNA=90°.
∵∠BAC=90°,
∴∠CAD=∠FAB=90°.
∵CE⊥BF
∴∠BEC=90°.
∵∠CFE=∠AFB.
∴∠ACD=∠ABF
在Rt△CAM和Rt△BAN中,
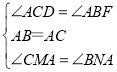 ,
,
∴Rt△CAM≌Rt△BAN
∴AM=AN
∵AM=AN, AM⊥CD, AN⊥BE
∴EA平分∠DEB
(3)∵CE⊥BF
∴∠BEC=90°.
∵∠CFE=∠AFB.
∴∠ACD=∠ABF
∵∠BAC=90°,
∴∠CAD=∠FAB=90°.
∵AC=AB
∴△CAD≌△BAF
∴AF=AD
设AD=AF=x
∵F为AC的中点
∴CF=AF=x,AC=2x
∴![]() ,AB=AC=2x
,AB=AC=2x
∵∠DCA=∠FCE,∠DAC=∠CEF=90°
∴![]()
∴![]()
∴![]()
解得![]()
∴![]()
∴![]()
∴DE=CD-CE=3
∴![]()
∴![]()

 快乐5加2金卷系列答案
快乐5加2金卷系列答案





