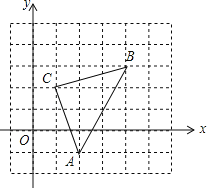
��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��A����5��0����B��5��0����D��2��7��������AD����y���ڵ�C��
��1����C�������� ����
��2������P��B�������ÿ��1����λ���ٶ���BA�����˶���ͬʱ����Q��C�������Ҳ��ÿ��1����λ���ٶ���y�������᷽���˶�����P���˶���A��ʱ�����㶼ֹͣ�˶�������ӳ������˶���x�룮
�����ú�x�Ĵ���ʽ�ֱ��ʾP��Q��������ꣻ
����x��2ʱ��y�����Ƿ����һ��E��ʹ�á�AQE��������APQ�������ȣ������ڣ���E�����꣬�������ڣ�˵�����ɣ�
��3���ڣ�2���������£��ڵ�P��Q�˶������У�����Q��x���ƽ����OF����G��F�ֱ�λ��y����������ࣩ����GQP���APQ�Ľ�ƽ���߽��ڵ�M�����PMQ�Ĵ�С�����P��Q���˶����仯��������仯���������PMQ�Ķ������������仯����˵�����ɣ�

���𰸡���1����0��5������2����P��5��x��0����Q��0��5+x���������ڣ���E������Ϊ��0��18.2����0����4.2������3����PMQ�Ķ������䣬ֵΪ90�㣮
��������
��1����DE��x�ᣬ���ݵ���������AE��DE��AO�����ݵ���ֱ�������ε����ʽ�ɣ�
��2���ٸ������⡢���ͼ�ν��
�ڷ�E��y����������E��y��ĸ�����������������������ε������ʽ���㼴�ɣ�
��3���ó���GQP+��APQ��180���������PQM+��QPM��90�������PMQ�Ķ������䣮
��1����DE��x�ᣬ
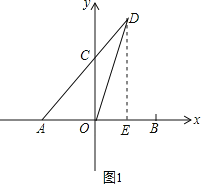
��A����5��0����D��2��7����
��AE��DE��7��AO��5��
�ߡ�CAO����DAEΪֱ�������Σ�
���CAO��45����
���CAO�ǵ���ֱ�������Σ�
��CO��AO��5��
��C��0��5����
�ʴ�Ϊ����0��5����
��2���١߶���P��B�������ÿ��1����λ���ٶ���BA�����˶���B��5��0����
��P��5��x��0����
�߶���Q��C�������ÿ��1����λ���ٶ���y�������᷽���˶���C��0��5����
��Q��0��5+x����
��P��5��x��0����Q��0��5+x����
�ڴ��ڣ���E������Ϊ��0��y����
��x��2ʱ��S��APQ����5+3����7��2��28��
���һ��E��y��������ᣮ
��y��7����5��2��28��
��y��18.2��
��E��0��18.2����
�������E��y��ĸ����ᣬ
��7��y����5��2��28��
��y����4.2��
��E��0����4.2����
���E����������0��18.2����0����4.2����
��3�����䣮

��GF��x�ᣬ
���GQP+��APQ��180����
��QM��PM�ֱ�ƽ�֡�GQP����APQ��
���PQM��![]() ��GQP����QPM��
��GQP����QPM��![]() ��APQ��
��APQ��
���PQM+��QPM��![]() ��GQP+
��GQP+![]() ��APQ��
��APQ��![]() ����GQP+��APQ����
����GQP+��APQ����![]() ��180����90����
��180����90����
�ߡ�PMQ+��PQM+��QPM��180����
���PMQ��180��������PQM+��QPM����180����90����90����
���PMQ�Ķ������䣮