Question

【题目】如图，已知⊙O的半径为2，AB为直径，CD为弦．AB与CD交于点M，将 沿CD翻折后，点A与圆心O重合，延长OA至P，使AP=OA，连接PC．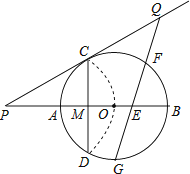
（1）求CD的长；
（2）求证：PC是⊙O的切线；
（3）点G为 的中点，在PC延长线上有一动点Q，连接QG交AB于点E．交 于点F（F与B、C不重合）．问GEGF是否为定值？如果是，求出该定值；如果不是，请说明理由．

Answer 1

【答案】
（1）

解：如图，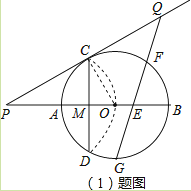

连接OC，

∵ 沿CD翻折后，点A与圆心O重合，

∴OM= OA= ×2=1，CD⊥OA，

∵OC=2，

∴CD=2CM=2 =2 =2 ．

（2）

证明：∵PA=OA=2，AM=OM=1，CM= CD= ，∠CMP=∠OMC=90°，

∴PC= = =2 ，

∵OC=2，PO=2+2=4，

∴PC2+OC2=（2 ）2+22=16=PO2，

∴∠PCO=90°，

∴PC是⊙O的切线．

（3）

解：GEGF是定值，证明如下：如图 ，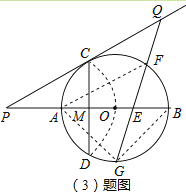

连接GA、AF、GB，

∵点G为 的中点，∴ = ，

∴∠BAG=∠AFG，

又∵∠AGE=∠FGA，

∴△AGE∽△FGA，

∴ = ，

∴GEGF=AG2，

∵AB为直径，AB=4，

∴∠BAG=∠ABG=45°，

∴AG=2 ，

∴GEGF=8．

【解析】（1）连接OC，根据翻折的性质求出OM，CD⊥OA，再利用勾股定理列式求解即可；
　　　　（2）利用勾股定理列式求出PC，然后利用勾股定理逆定理求出∠PCO=90°，再根据圆的切线的定义证明即可；
　　　　（3）连接GA、AF、GB，根据等弧所对的圆周角相等可得∠BAG=∠AFG，然后根据两组角对应相等两三角相似求出△AGE和△FGA相似，根据相似三角形对应边成比例可得 = ，从而得到GEGF=AG2 ， 再根据等腰直角三角形的性质求解即可． 本题是圆的综合题型，主要利用了翻折变换的性质，垂径定理，勾股定理，勾股定理逆定理，圆的切线的定义，相似三角形的判定与性质，难点在于（3）作辅助线构造出相似三角形．