题目内容
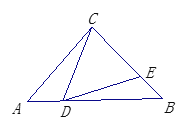
【题目】如图,![]() ABC是等边三角形,点D是线段AC上的一动点,E在BC的延长线上,且BD=DE.
ABC是等边三角形,点D是线段AC上的一动点,E在BC的延长线上,且BD=DE.
(1)如图,若点D为线段AC的中点,求证:AD=CE;
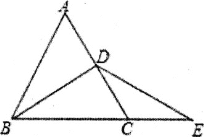
(2)如图,若点D为线段AC上任意一点,求证:AD=CE.

【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)根据等边三角形三线合一的性质即可求得∠DBC的度数,根据BD=DE即可解题;
(2)作DF∥AB,可证△BDF≌△EDC,可得BF=CE,再证AD=BF即可解题.
(1)∵点D为等边三角形△ABC边AC的中点,
∴BD平分∠ABC,AD=DC
∴∠DBE=30°,
∵BD=DE,
∴∠E=∠DBE=30°,
∵∠DCE=180°-∠ACB=120°,
∴∠CDE=180°-120°-30°=30°,
∴∠CDE=∠E =30°∴DC=CE
∴AD=CE;………………4分

(2)作DF∥AB,可得△DFC是等边三角形,∴DC=CF
∴AC-DC=BC-CF ∴AD=BF
在△BDF和△EDC中,
∴△BDF≌△EDC,(AAS)
∴BF=CE,
∴AD=CE.

练习册系列答案
相关题目