Question

【题目】如图，某抛物线的对称轴为直线x=2，点E是该抛物线顶点，抛物线与y轴交于点C，过点C作CD∥x轴，与抛物线交于点B，与对称轴交于点D，点A是对称轴上一点，连结AC，AB，若△ABC是等边三角形，则图中阴影部分图形的面积之和是 ．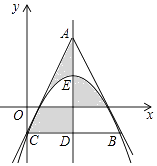

Answer 1

【答案】2
【解析】解：
∵对称轴为直线x=2，
∴CD=2，
∵△ABC为等边三角形，
∴AC=BC=2CD=4，
在Rt△ACD中，AD=2 ，
∴S△ACD= S△ABC= ×× ×4×2 =2 ，
由抛物线的对称性可知S阴影=S△ACD=2 ，
故答案为：2 ．
由抛物线的对称性可知阴影部分面积之和等于△ABC的一半，由对称轴为x=2可求得CB的长，则可求得△ABC的面积，则可求得答案．