Question

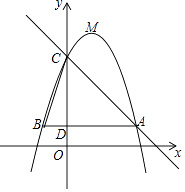
【题目】如图，抛物线y=﹣x2+mx+n与x轴交于A，B两点，y与轴交于点C，抛物线的对称轴交x轴于点D．已知A（﹣1，0），C（0，3）

（1）求抛物线的解析式；
（2）在抛物线的对称轴上是否存在P点，使△PCD是以CD为腰的等腰三角形，如果存在，直接写出点P的坐标，如果不存在，请说明理由；
（3）点E是线段BC上的一个动点，过点E作x轴的垂线与抛物线相交于点F，
①求直线BC 的解析式；
②当点E运动到什么位置时，四边形CDBF的面积最大？求四边形CDBF的最大面积及此时点E的坐标．

Answer 1

【答案】
（1）

解：∵抛物线y=﹣ x2+mx+n经过A（﹣1，0），C（0，2）．

解得： ，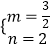

∴抛物线的解析式为：y=﹣ x2+ x+2

（2）

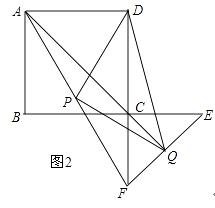
解：如图1，∵y=﹣ x2+ x+2，

∴y=﹣ （x﹣ ）2+ ，

∴抛物线的对称轴是直线x= ．

∴OD= ．

∵C（0，2），

∴OC=2．

在Rt△OCD中，由勾股定理，得CD= ．

∵△CDP是以CD为腰的等腰三角形，

∴CP1=DP2=DP3．

作CH⊥x轴于H，

∴HP1=HD=2，

∴DP1=4．

∴P1（ ，4），P2（ ， ），P3（ ，﹣ ）

（3）

解：当y=0时，0=﹣ x2+ x+2

∴x1=﹣1，x2=4，

∴B（4，0）．

设直线BC的解析式为y=kx+b，由图象，得

，

解得： ，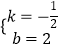

∴直线BC的解析式为：y=﹣ x+2．

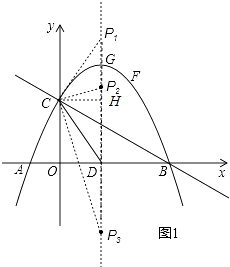
如图2，过点C作CM⊥EF于M，设E（a，﹣ a+2），F（a，﹣ a2+ a+2），

∴EF=﹣ a2+ a+2﹣（﹣ a+2）=﹣ a2+2a（0≤x≤4）．

∵S四边形CDBF=S△BCD+S△CEF+S△BEF= BDOC+ EFCM+ EFBN，

= ×2+ a（﹣ a2+2a）+ （4﹣a）（﹣ a2+2a），

=﹣a2+4a+ （0≤x≤4）．

=﹣（a﹣2）2+

∴a=2时，S四边形CDBF的面积最大= ，

∴E（2，1）．

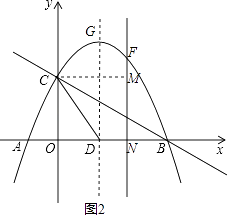
【解析】（1）由待定系数法建立二元一次方程组求出m、n的值即可；（2）如图1中，分两种情形讨论①当PD=DC时，当CP=CD时，分别写出点P坐标即可．（3）先求出BC的解析式，设出点E的横坐标为a，由四边形CDBF的面积=S△BCD+S△CEF+S△BEF求出S与a的关系式，由二次函数的性质就可以求出结论．
【考点精析】认真审题，首先需要了解二次函数的图象(二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点)，还要掌握二次函数的性质(增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小)的相关知识才是答题的关键．