题目内容
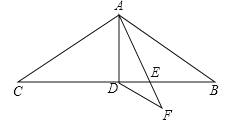
【题目】如图在△ABC中,AB=AC=9,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,求DF的长.
【答案】4.5.
【解析】
试题分析:由等腰三角形三线合一的性质可得AD⊥BC,∠BAD=∠CAD,再求出∠DAE=∠EAB=30°,然后由平行线的性质求出∠F=∠BAE=30°,从而得到∠DAE=∠F,再由等角对等边求出AD=DF,然后求出∠B=30°,由直角三角形30°角所对的直角边等于斜边的一半解答.
试题解析:解:∵AB=AC,AD是△ABC的中线,∴AD⊥BC,∠BAD=∠CAD=![]() ∠BAC=
∠BAC=![]() ×120°=60°,∵AE是∠BAD的角平分线,∴∠DAE=∠EAB=
×120°=60°,∵AE是∠BAD的角平分线,∴∠DAE=∠EAB=![]() ∠BAD=
∠BAD=![]() ×60°=30°,∵DF∥AB,∴∠F=∠BAE=30°,∴∠DAE=∠F=30°,∴AD=DF,∵∠B=90°﹣60°=30°,∴AD=
×60°=30°,∵DF∥AB,∴∠F=∠BAE=30°,∴∠DAE=∠F=30°,∴AD=DF,∵∠B=90°﹣60°=30°,∴AD=![]() AB=
AB=![]() ×9=4.5,∴DF=4.5.
×9=4.5,∴DF=4.5.

练习册系列答案
相关题目