题目内容
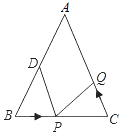
【题目】如图.在数学活动课中,小明剪了一张△ABC的纸片,其中∠A=60°,他将△ABC折叠压平使点A落在点B处,折痕DE,D在AB上,E在AC上.
(1)请作出折痕DE;(要求:尺规作图,不写作法,保留作图痕迹)
(2)判断△ABE的形状并说明;
(3)若AE=5,△BCE的周长为12,求△ABC的周长.

【答案】(1)见解析;(2)△ABE是等边三角形;(3)17;
【解析】
(1)作AB的垂直平分线DE,垂足为D,交AC于E,DE即为所求;
(2)由线段垂直平分线的性质得出AE=BE,由∠A=60°,即可得出△ABE是等边三角形;
(3)由三角形的周长和AE=BE得出BC+AC=13,由等边三角形的性质得出AB=AE=6,即可得出△ABC的周长.
解:(1)根据题意得:
作AB的垂直平分线DE,垂足为D,交AC于E,DE即为所求,如图1所示:
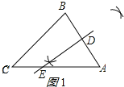
(2)△ABE是等边三角形,理由如下:
如图2所示:
∵DE是AB的垂直平分线,
∴AE=BE,
∵∠A=60°,
∴△ABE是等边三角形;
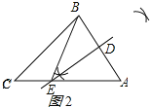
(3)∵△BCE的周长为12,
∴BC+BE+CE=12,
∵AE=BE,
∴BC+AC=12,
∵△ABE是等边三角形,
∴AB=AE=5,
∴△ABC的周长=AB+BC+AC
=5+12=17.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目