题目内容
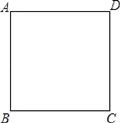
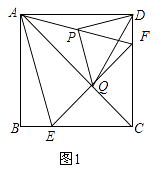
【题目】如图,已知正方形ABCD的边长为10厘米,点E在边AB上,且AE=4厘米,如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.设运动时间为t秒.
(1)若点Q的运动速度与点P的运动速度相等,经过2秒后,△BPE与△CQP是否全等?请说明理由;
(2)若点Q的运动速度与点P的运动速度不相等,则当t为何值时,能够使△BPE与△CQP全等;此时点Q的运动速度为多少.

【答案】(1)△BPE与△CQP全等,理由见解析;(2)t=![]() ,
,
【解析】
(1)根据SAS可判定全等;
(2)由于点Q的运动速度与点P的运动速度不相等,而运动时间相同,所以BP≠CQ.又△BPE与△CQP全等,则有BP=PC=![]() BC=5,CQ=BE=6,由BP=5求出运动时间,再根据速度=路程÷时间,即可得出点Q的速度.
BC=5,CQ=BE=6,由BP=5求出运动时间,再根据速度=路程÷时间,即可得出点Q的速度.
(1)△BPE与△CQP全等.
∵点Q的运动速度与点P的运动速度相等,且t=2秒,
∴BP=CQ=2×2=4厘米,
∵AB=BC=10厘米,AE=4厘米,
∴BE=CP=6厘米,
∵四边形ABCD是正方形,
∴在Rt△BPE和Rt△CQP中,![]() ,
,
∴Rt△BPE≌Rt△CQP;
(2)∵点Q的运动速度与点P的运动速度不相等,
∴BP≠CQ,
∵∠B=∠C=90°,
∴要使△BPE与△OQP全等,只要BP=PC=5厘米,CQ=BE=6厘米,即可.
∴点P,Q运动的时间t=![]() (秒)
(秒)
此时点Q的运动速度为![]() (厘米/秒).
(厘米/秒).

【题目】深圳市政府计划投资1.4万亿元实施东进战略.为了解深圳市民对东进战略的关注情况.某校数学兴趣小组随机采访部分深圳市民,对采访情况制作了统计图表的一部分如下:
关注情况 | 频数 | 频率 |
A.高度关注 | M | 0.1 |
B.一般关注 | 100 | 0.5 |
C.不关注 | 30 | N |
D.不知道 | 50 | 0.25 |
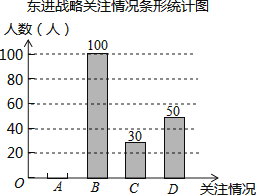
(1)根据上述统计图可得此次采访的人数为人,m= , n=
(2)根据以上信息补全条形统计图;
(3)根据上述采访结果,请估计在15000名深圳市民中,高度关注东进战略的深圳市民约有人.