Question

如图，直角坐标系中，已知点A（2，4），B（5，0），动点P从B点出发沿BO向终点O运动，动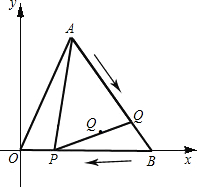点Q从A点出发沿AB向终点B运动．两点同时出发，速度均为每秒1个单位，设从出发起运动了xs．
（1）Q点的坐标为______（用含x的代数式表示）；
（2）当x为何值时，△APQ是一个以AP为腰的等腰三角形？
（3）记PQ的中点为G．请你探求点G随点P，Q运动所形成的图形，并说明理由．

Answer 1

（1）（2+

3

5

x，4-

4

5

x）．

（2）由题意，得P（5-x，0），0＜x≤5
由勾股定理
求得PQ²=（

8

5

x-3）²+（4-

4

5

x）²
AP²=（3-x）²+4²
若AQ=AP，则x²=（3-x）²+4²，解得x=

25

6

若PQ=AP
则（

8

5

x-3）²+（4-

4

5

x）²=（3-x）²+4²
即

11

5

x²-10x=0，解得x₁=0（舍去），x₂=

50

11

经检验，当x=

25

6

或x=

50

11

时，△APQ是一个以AP为腰的等腰三角形．

（3）设AB、BO的中点分别为点M、N，则点G随点P、Q运动所形成的图形是线段MN
设MN，PQ相交于点G′，过点P作PK∥AO交AB于点K

∴PK∥AO∥MN
∴△A0B∽△KPB∽△MNB．
∵AB=OB
∴BK=BP=AQ，BM=BN
∴BK-BM=AQ-BM，
BK-BM=AQ-AM
即KM=QM
∴PG′=QG′
∴G′是PQ的中点
即点G′与点G重合．
∴点G随点P、Q运动所形成的图形是△OBA的中位线MN．