题目内容
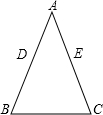
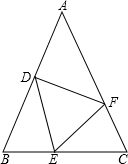
如图，△ABC中，AB=AC，D，E，F分别为AB，BC，CA上的点，且BD=CE，∠DEF=∠B
（1）求证：△BDE≌△CEF；
（2）若∠A=40°，求∠EDF的度数．
（1）求证：△BDE≌△CEF；
（2）若∠A=40°，求∠EDF的度数．
（1）证明：∵∠DEC=∠B+∠BDE=∠CEF+∠DEF，∠DEF=∠B，
∴∠CEF=∠BDE．
∵AB=AC，
∴∠C=∠B．
又∵CE=BD，
∴△BDE≌△CEF．
（2）∵△BDE≌△CEF
∴DE=FE．
所以△DEF是等腰三角形．
∴∠EDF=∠EFD
又，△ABC中，AB=AC，∠A=40°
∴∠B=70°，
已知∠DEF=∠B
∴∠DEF=70°
∴∠EDF=∠EFD=
×（180°-70°）=55°．
∴∠CEF=∠BDE．
∵AB=AC，
∴∠C=∠B．
又∵CE=BD，
∴△BDE≌△CEF．
（2）∵△BDE≌△CEF
∴DE=FE．
所以△DEF是等腰三角形．
∴∠EDF=∠EFD
又，△ABC中，AB=AC，∠A=40°
∴∠B=70°，
已知∠DEF=∠B
∴∠DEF=70°
∴∠EDF=∠EFD=
| 1 |
| 2 |
练习册系列答案
相关题目
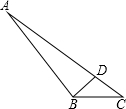
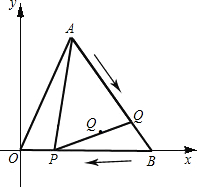点Q从A点出发沿AB向终点B运动．两点同时出发，速度均为每秒1个单位，设从出发起运动了xs．
