题目内容
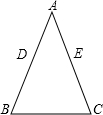
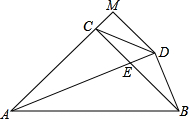
如图，在△ABC中，AB=AC，AD=DC=BC，求∠A的度数．
∵AB=AC，AD=DC=BC，
∴A=∠ACD，∠B=∠ACB=∠CDB，
设∠A=x°，则∠ACD=x°，
∴∠B=∠ACB=∠CDB=2x°，
∵∠A+∠B+∠ACB=180°，
∴x+2x+2x=180，
解得x=36．
故等腰三角形ABC的顶角∠A度数为36°．
∴A=∠ACD，∠B=∠ACB=∠CDB，
设∠A=x°，则∠ACD=x°，
∴∠B=∠ACB=∠CDB=2x°，
∵∠A+∠B+∠ACB=180°，
∴x+2x+2x=180，
解得x=36．
故等腰三角形ABC的顶角∠A度数为36°．
练习册系列答案
相关题目
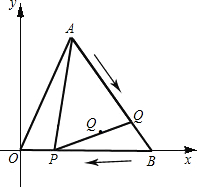点Q从A点出发沿AB向终点B运动．两点同时出发，速度均为每秒1个单位，设从出发起运动了xs．
