题目内容
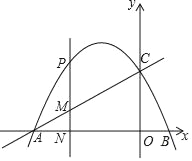
【题目】如图1所示,在平面直角坐标系中,![]() 、
、![]() 、
、![]() ,其中
,其中![]() 、
、![]() 满足关系式
满足关系式![]() ,平移
,平移![]() 使点
使点![]() 与点
与点![]() 重合,点
重合,点![]() 的对应点为点
的对应点为点![]() .
.
(1)直接写出![]() 、
、![]() 两点的坐标,则
两点的坐标,则![]() (______,______)、
(______,______)、![]() (______,______).
(______,______).
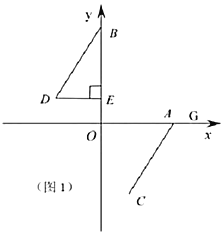
(2)如图1,过点![]() 作
作![]() 轴交于
轴交于![]() 点,猜想
点,猜想![]() 与
与![]() 数量关系,并说明理由.
数量关系,并说明理由.
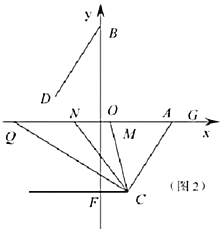
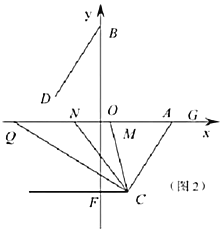
(3)如图2,过点![]() 作
作![]() 轴交
轴交![]() 轴于
轴于![]() 点,
点,![]() 为
为![]() 轴上点
轴上点![]() 左侧的一动点,连接
左侧的一动点,连接![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,当点
,当点![]() 运动时,
运动时,![]() 的值是否变化?如果变化,请说明理由;如果不变,请求出其值.
的值是否变化?如果变化,请说明理由;如果不变,请求出其值.
【答案】(1)3;0;-2;1;(2)互补,理由见解析;(3)不变;![]() .
.
【解析】
(1)根据算术平方根的非负性和平方的非负性即可求出a、b的值,从而求出A、B的坐标,再根据A、B的坐标即可发现点A到点B的平移规律,从而得到:点C到点D的平移规律,即可求出D点坐标;
(2)延长DE和CA交于点P,根据平行线的性质即可证出:![]() =∠P=∠OAC,然后根据平角的定义即可得:∠OAC+∠CAG=180°,从而得到:
=∠P=∠OAC,然后根据平角的定义即可得:∠OAC+∠CAG=180°,从而得到:![]() 与
与![]() 互补;
互补;
(3)根据角平分线的定义可得:∠ACM=![]() ,∠ACN=
,∠ACN=![]() ,从而得出∠MCN=∠ACN-∠ACM=
,从而得出∠MCN=∠ACN-∠ACM=![]() ,再根据平行线的性质可得:∠AQC=∠FCQ,即可求出
,再根据平行线的性质可得:∠AQC=∠FCQ,即可求出![]() 的值.
的值.
解:(1)∵![]()
∴![]()
解得:![]()
∴点A坐标为:(3,0),点B的坐标为:(0,4)
∵平移![]() 使点
使点![]() 与点
与点![]() 重合,点
重合,点![]() 的对应点为点
的对应点为点![]() ,
,
由坐标可知:点A到点B的平移规律为:先向左平移3个单位,再向上平移4个单位
∴点C到点D的平移规律为:先向左平移3个单位,再向上平移4个单位
∴点D的坐标为:(1-3,﹣3+4)=(-2,1);
(2)互补,理由如下,
延长DE和CA交于点P,如下图所示
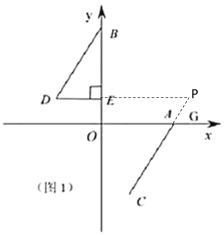
∵BD∥CA
∴![]() =∠P
=∠P
∵DE⊥y轴
∴DE∥x轴
∴![]() =∠P=∠OAC
=∠P=∠OAC
∵∠OAC+∠CAG=180°
∴![]() +∠CAG=180°
+∠CAG=180°
∴![]() 与
与![]() 互补;
互补;
(3)不变,
∵![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,
∴∠ACM=![]() ,∠ACN=
,∠ACN=![]() ,
,
∴∠MCN=∠ACN-∠ACM=![]() -
-![]() =
=![]() =
=![]() ,
,
∵![]() 轴,
轴,
∴∠AQC=∠FCQ,
∴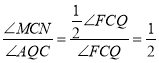 .
.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案【题目】从2012年7月1日起某市执行新版居民阶梯电价,小明同学家收到了新政后的第一张电费单,小明爸爸说:“小明,请你计算一下,这个月的电费支出与新政前相比是多了还是少了?”于是小明上网了解了有关电费的收费情况,得到如下两表:
2004年1月至2012年6月执行的收费标准:
月用电量(度)50度有以下部分 | 50度有以下部分 | 超过50度但不超过200度部分 | 超过200度以上部分 |
单价(元/度) | 0.53 | 0.56 | 0.63 |
2012年7月起执行的收费标准:
月用电量(度) | 230度有以下部分 | 超过230度但不超过400度部分 | 超过400度以上部分 |
单价(元/度) | 0.53 | 0.58 | 0.83 |
(1)若小明家2012年7月份的用电量为200度,则小明家7月份的电费支出是多少元?比新政前少了多少元?
(2)若新政后小明家的月用电量为a度,请你用含a的代数式表示当月的电费支出.