题目内容
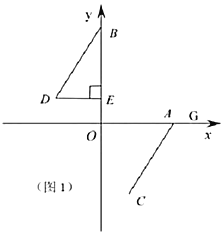
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.D,E分别为边BC,AC上一点,将△ADE沿着直线AD翻折,点E落在点F处,如果DF⊥BC,△AEF是等边三角形,那么AE=_____.

【答案】4.
【解析】
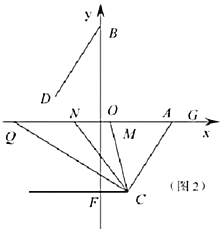
由题意可得∠CAD=30°,∠AEF=60°,根据勾股定理可求CD=2![]() ,由AC∥DF,则∠AEF=∠EFD=60°,且DE=DF,可得∠DEF=∠DFE=60°,可得∠DEC=60°.根据勾股定理可求EC的长,即可求AE的长.
,由AC∥DF,则∠AEF=∠EFD=60°,且DE=DF,可得∠DEF=∠DFE=60°,可得∠DEC=60°.根据勾股定理可求EC的长,即可求AE的长.
如图:

∵折叠,
∴∠EAD=∠FAD,DE=DF,
∴∠DFE=∠DEF;
∵△AEF是等边三角形,
∴∠EAF=∠AEF=60°,
∴∠EAD=∠FAD=30°;
在Rt△ACD中,AC=6,∠CAD=30°,
∴CD=2![]() ;
;
∵FD⊥BC,AC⊥BC,
∴AC∥DF,
∴∠AEF=∠EFD=60°,
∴∠FED=60°;
∵∠AEF+∠DEC+∠DEF=180°,
∴∠DEC=60°;
∵在Rt△DEC中,∠DEC=60°,CD=2![]() ,
,
∴EC=2;
∵AE=AC﹣EC,
∴AE=6﹣2=4;
故答案为:4.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
【题目】某区举行“中华诵![]() 经典诵读”大赛,小学、中学组根据初赛成绩,各选出5名选手组成小学代表队和中学代表队参加市级决赛,两个代表队各选出的5名选手的决赛成绩分别绘制成下列两个统计图
经典诵读”大赛,小学、中学组根据初赛成绩,各选出5名选手组成小学代表队和中学代表队参加市级决赛,两个代表队各选出的5名选手的决赛成绩分别绘制成下列两个统计图

根据以上信息,整理分析数据如下:
平均数(分 | 中位数(分 | 众数(分 | |
小学组 | 85 |
| 100 |
中学组 |
| 85 |
|
(1)写出表格中![]() ,
,![]() ,
,![]() 的值:
的值:![]() ,
,![]() ,
,![]() .
.
(2)结合两队成绩的平均数和中位数进行分析,哪个队的决赛成绩较好?
(3)计算两队决赛成绩的方差,并判断哪一个代表队选手成绩较稳定.