题目内容
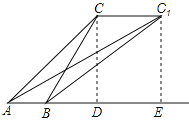
【题目】如图：两个观察者从A，B两地观测空中C处一个气球，分别测得仰角为45°和60°，已知A，B两地相距200m，当气球沿着与AB平行地漂移40秒后到达C1，在A处测得气球的仰角为30度．
求：（1）气球漂移的平均速度（结果保留3个有效数字）；
（2）在B处观测点C1的仰角（精确到度）．
【答案】（1）速度为200
÷40≈8.66m/s；（2）仰角为37°．
【解析】试题分析：首先分析图形：根据题意构造直角三角形；本题涉及到两个直角三角形，应利用其公共边构造等量关系，进而可求出答案．
试题解析：解：（1）作CD⊥AB，C1E⊥AB，垂足分别为D、E．在Rt△ACD中，AD=CD÷tan∠CAD=CD÷tan45°=CD；在Rt△BCD中，BD=CD÷tan∠CBD=CD÷tan60°=
；
又因为AB=AD﹣BD=200，所以CD﹣=200，解得：CD=100（3
），又CD⊥AB，C1E⊥AB，CC1∥AB，所以C1E=CD，DE=CC1．在Rt△AEC1中，AE=C1E÷tan∠C1AE=100（3+
）÷tan30°=300（
），所以CC1=DE=AE﹣AD=300（）﹣100（3+），即CC1=200，速度为200÷40≈8.66m/s；
（2）由（1）知BD==100（1），所以tan∠C1BE=
=
≈0.7637，所以∠C1BE=37°，即仰角为37°．
【题目】某区举行“中华诵
经典诵读”大赛，小学、中学组根据初赛成绩，各选出5名选手组成小学代表队和中学代表队参加市级决赛，两个代表队各选出的5名选手的决赛成绩分别绘制成下列两个统计图
根据以上信息，整理分析数据如下：
平均数（分 | 中位数（分 | 众数（分 | |
小学组 | 85 |
| 100 |
中学组 |
| 85 |
|
（1）写出表格中
，
，
的值：
，
，
．
（2）结合两队成绩的平均数和中位数进行分析，哪个队的决赛成绩较好？
（3）计算两队决赛成绩的方差，并判断哪一个代表队选手成绩较稳定．
