题目内容
如图1,在?ABCD中,∠BCD的平分线交直线AD于点F,∠BAD的平分线交DC延长线于E.
(1)在图1中,证明AF=EC;
(2)若∠BAD=90°,G为CF的中点(如图2),判断△BEG的形状,并证明.

(1)在图1中,证明AF=EC;
(2)若∠BAD=90°,G为CF的中点(如图2),判断△BEG的形状,并证明.

(1)证明:∵四边形ABCD是平行四边形,
∴BC∥AD,∠BAD=∠BCD,
∵∠BCD的平分线CF,∠BAD的平分线AM,
∴∠4=
∠BAD,∠2=∠3=
∠BCD,
∴∠2=∠3=∠4,
∵BC∥AD,
∴∠1=∠4,
∴∠1=∠2,
∴AM∥CF,
即AE∥CF,AE≠CF,
∴四边形AECF是梯形,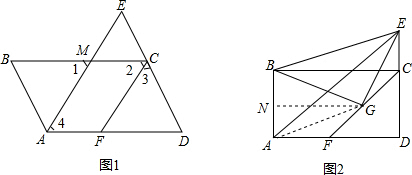
∵AM∥CF,
∴∠3=∠E=∠4,
∴梯形AECF是等腰梯形,
∴AF=CE;
(2)△BEG是等腰直角三角形,
证明:连接AG,过G作GN∥BC交AB于N,
∵四边形ABCD是矩形,
∴BC∥AD,∠CBN=90°,
∴∠GNB=90°,BC∥GN∥AD,
∵G为CF的中点,
∴N为AB中点,
即NG是AB的垂直平分线,
∴BG=AG,
∴∠BGN=∠AGN,
∵NG∥AD,
∴∠AGN=∠GAF=∠BGN,
∵CF平分∠BCD,∠BCD=90°,
∴∠DCF=90°,∠DCF=45°,
∴∠DFC=45°,
∴∠ECG=∠AFC=90°+45°=135°,
在△AFG和△ECG中
∵
,
∴△AFG≌△ECG(SAS),
∴AG=EG=BG,∠EGC=∠AGF,∠GAF=∠GEC,
∵∠AGN=∠GAF=∠BGN,
∴∠AGN=∠GAF=∠BGN=∠GEC,
∵∠GAF+∠AGF=180°-135°=45°,
∴∠EGC+∠BGF=2(∠GAF+∠AGF)=90°
∴△BEG是等腰直角三角形.
∴BC∥AD,∠BAD=∠BCD,
∵∠BCD的平分线CF,∠BAD的平分线AM,
∴∠4=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠2=∠3=∠4,
∵BC∥AD,
∴∠1=∠4,
∴∠1=∠2,
∴AM∥CF,
即AE∥CF,AE≠CF,
∴四边形AECF是梯形,
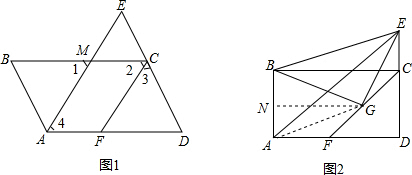
∵AM∥CF,
∴∠3=∠E=∠4,
∴梯形AECF是等腰梯形,
∴AF=CE;
(2)△BEG是等腰直角三角形,
证明:连接AG,过G作GN∥BC交AB于N,
∵四边形ABCD是矩形,
∴BC∥AD,∠CBN=90°,
∴∠GNB=90°,BC∥GN∥AD,
∵G为CF的中点,
∴N为AB中点,
即NG是AB的垂直平分线,
∴BG=AG,
∴∠BGN=∠AGN,
∵NG∥AD,
∴∠AGN=∠GAF=∠BGN,
∵CF平分∠BCD,∠BCD=90°,
∴∠DCF=90°,∠DCF=45°,
∴∠DFC=45°,
∴∠ECG=∠AFC=90°+45°=135°,
在△AFG和△ECG中
∵
|
∴△AFG≌△ECG(SAS),
∴AG=EG=BG,∠EGC=∠AGF,∠GAF=∠GEC,
∵∠AGN=∠GAF=∠BGN,
∴∠AGN=∠GAF=∠BGN=∠GEC,
∵∠GAF+∠AGF=180°-135°=45°,
∴∠EGC+∠BGF=2(∠GAF+∠AGF)=90°
∴△BEG是等腰直角三角形.

练习册系列答案
相关题目


 比△DOC的周长小10cm.
比△DOC的周长小10cm.