题目内容
如图，在平行四边形ABCD中，DE⊥AB于E，DF⊥BC于F，平行四边形ABCD的周长是36，DE=4
，DF=5
．
（1）求AB，BC的长；
（2）求∠A，∠B的度数．
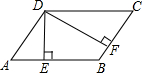
| 3 |
| 3 |
（1）求AB，BC的长；
（2）求∠A，∠B的度数．
（1）在平行四边形ABCD中，
∵AB=CD，AD=BC．
∴AB+BC=
=18
根据平行四边形的面积公式得：S?ABCD=AB•DE=BC•DF，
∴AB：BC=DF：DE=5：4．
∴AB=10，BC=8．
（2）在直角三角形ADE中，AD=BC=8，DE=4
，
∴sinA=
=
．
∴∠A=60°，∠B=120°．
∵AB=CD，AD=BC．
∴AB+BC=
| 36 |
| 2 |
根据平行四边形的面积公式得：S?ABCD=AB•DE=BC•DF，
∴AB：BC=DF：DE=5：4．
∴AB=10，BC=8．
（2）在直角三角形ADE中，AD=BC=8，DE=4
| 3 |
∴sinA=
| DE |
| AD |
| ||
| 2 |
∴∠A=60°，∠B=120°．
练习册系列答案
冲刺100分1号卷系列答案
相关题目
