��Ŀ����
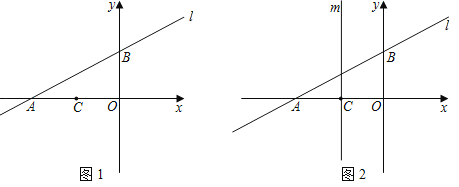
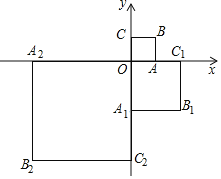
����Ŀ���ں�����ѧϰ�У����Ǿ�������ȷ����������ʽ��������ͼ�����ú���ͼ���о��������ʩ�����ͼ������������ѧϰ���̣��ڻ�����ͼ��ʱ�����dz���ͨ������ƽ�ƻ��۵ķ���������ͼ��С������ѧ���ĺ���֪ʶ̽������y1��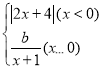 ��ͼ�������ʲ�����ͼ�������⣮С���г������y1��x�ļ����Ӧ��ֵ��
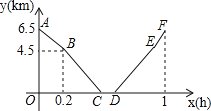
��ͼ�������ʲ�����ͼ�������⣮С���г������y1��x�ļ����Ӧ��ֵ��
x | �� | ��4 | ��3 | ��2 | ��1 | 0 | 1 | 2 | 3 | 4 | �� |
y1 | �� | 4 | 2 | m | 2 | 4 | 2 |
| n |
| �� |
��1�����ݱ�����x��y1�Ķ�Ӧ��ϵ�ɵ�m��______��n��______��
��2����ƽ��ֱ������ϵ�У���������и��㣬�����ú���ͼ���ݺ���ͼ��д���ú�����һ������______��
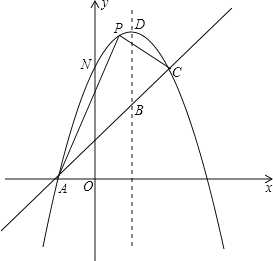
��3��������y1��ͼ����ֱ��y2��mx+1����������ʱ��ֱ��д��m��ȡֵ��Χ��
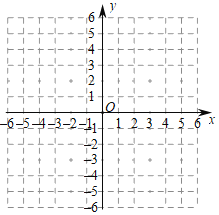
���𰸡���1��0��1����2����x����2ʱ��y��x�����Ӷ���С����2��x��0ʱ��y��x�����Ӷ�����x��0ʱ��y��x�����Ӷ���С����3��0��m��![]() ��-7+4
��-7+4![]() ��
��
��������
��1�����ݱ�����Ϣ�����ô���ϵ����������⼴�ɣ�
��2��������㷨��������ͼ�ɣ����ͼ���������������ʼ��ɣ�
��3���жϳ�ֱ����˫�����н����m��ȡֵ��Χ�������ֱ�߾�������2��0��ʱm��ֵ�����жϣ�
��1����y1��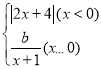 ��
��
��x����2ʱ��m��|2������2��+4|��0��
��x��0ʱ��y1��4��
��b��4��
��x��3ʱ��n��1��
�ʴ�Ϊ��0��1��
��2������ͼ����ͼ��ʾ��ͼ��ʵ�ߣ���
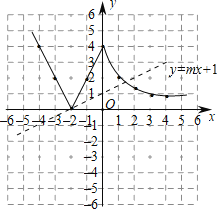
���ʣ��ٵ�x����2ʱ��y��x�����Ӷ���С��
�ڵ���2��x��0ʱ��y��x�����Ӷ�����
�۵�x��0ʱ��y��x�����Ӷ���С��
�ʴ�Ϊ����x����2ʱ��y��x�����Ӷ���С����2��x��0ʱ��y��x�����Ӷ�����x��0ʱ��y��x�����Ӷ���С��
��3����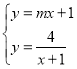 ����ȥy�õ���mx2+(m+1)x��3��0��
����ȥy�õ���mx2+(m+1)x��3��0��
����=0ʱ��m2+14m+1=0��
���m=-7+3![]() ��-7-4
��-7-4![]() ����������
����������
��ֱ��y=mx+1������-2��0��ʱ��m=![]() ��
��
�۲�ͼ���֪������y1��ͼ����ֱ��y2=m+1����������ʱ��m��ȡֵ��Χ0��m��![]() ��-7+4
��-7+4![]() ��
��