题目内容
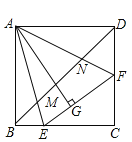
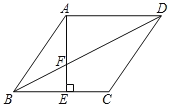
【题目】菱形ABCD中,AE⊥BC于E,交BD于F点,下列结论:
①BF为∠ABE的角平分线;
②DF=2BF;
③2AB2=DFDB;
④sin∠BAE=![]() .其中正确的为( )
.其中正确的为( )
A.①③B.①②④C.①④D.①③④
【答案】D
【解析】
由四边形ABCD是菱形,即可得BF为∠ABE的角平分线;可得①正确;由当∠ABC=60°时,DF=2BF,可得②错误;连接AC,易证得△AOD∽△FAD,由相似三角形的对应边成比例,可证得AD:DF=OD:AD,继而可得2AB2=DFDB,即④正确;连接FC,易证得△ABF≌△CBF(SAS),可得∠BCF=∠BAE,AF=CF,然后由正弦函数的定义,可求得④正确.
解:①∵四边形ABCD是菱形,∴BF为∠ABE的角平分线,
故①正确;
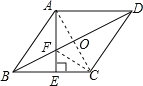
②连接AC交BD于点O.
∵四边形ABCD是菱形,∴AB=BC=AD,∴当∠ABC=60°时,△ABC是等边三角形,
即AB=AC,
则DF=2BF.
∵∠ABC的度数不定,∴DF不一定等于2BF;
故②错误;
③∵AE⊥BC,AD∥BC,∴AE⊥AD,∴∠FAD=90°.
∵四边形ABCD是菱形,∴AC⊥BD,OB=OD=![]() DB,AD=AB,∴∠AOD=∠FAD=90°.
DB,AD=AB,∴∠AOD=∠FAD=90°.
∵∠ADO=∠FDO,∴△AOD∽△FAD,∴AD:DF=OD:AD,∴AD2=DFOD,∴AB2=DF![]() DB,
DB,
即2AB2=DFDB;
故③正确;
④连接CF,
在△ABF和△CBF中, ∴△ABF≌△CBF(SAS),∴∠BCF=∠BAE,AF=CF,
∴△ABF≌△CBF(SAS),∴∠BCF=∠BAE,AF=CF,
在Rt△EFC中,sin∠ECF=![]() =
=![]() ,∴sin∠BAE=
,∴sin∠BAE=![]() .
.
故④正确.
故选:D.

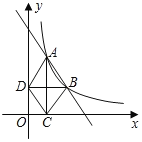
【题目】在函数的学习中,我们经历了“确定函数表法式﹣画函数图象﹣利用函数图象研究函数性质﹣利用图象解决问题”的学习过程.在画函数图象时,我们常常通过描点或平移或翻折的方法画函数图象.小明根据学到的函数知识探究函数y1=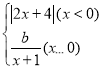 的图象与性质并利用图象解决问题.小明列出了如表y1与x的几组对应的值:
的图象与性质并利用图象解决问题.小明列出了如表y1与x的几组对应的值:
x | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
y1 | … | 4 | 2 | m | 2 | 4 | 2 |
| n |
| … |
(1)根据表格中x、y1的对应关系可得m=______,n=______;
(2)在平面直角坐标系中,描出表格中各点,两出该函数图象;根据函数图象,写出该函数的一条性质______.
(3)当函数y1的图象与直线y2=mx+1有三个交点时,直接写出m的取值范围.