题目内容
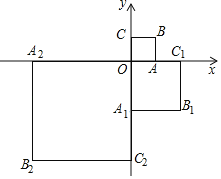
【题目】如图，在平面直角坐标系xOy中，正方形OABC的顶点A、C分别在x，y轴上，且AO＝1．将正方形OABC绕原点O顺时针旋转90°，且A1O＝2AO，得到正方形OA1B1C1，再将正方OA1B1C1绕原点O顺时针旋转90°，且A2O＝2A1O，得到正方形OA2B2C2…以此规律，得到正方形OA2019B2019C2019，则点B2019的坐标为_____．
【答案】(﹣22019，22019)
【解析】
根据题意得出B点坐标变化规律，进而得出点B2019的坐标位置，进而得出答案．
解：∵四边形OABC是正方形，OA＝1，
∴AB＝OA＝1，
∴B（1，1），
将正方形OABC绕原点O顺时针旋转90°，
且A1O＝2AO，得到正方形OA1B1C1，
再将正方OA1B1C1绕原点O顺时针旋转90°，
且A2O＝2A1O，得到正方形OA2B2C2…以此规律，
∴每4次循环一周，B1（2，﹣2），B2（﹣4，﹣4），B3（﹣8，8），B4（16，16），
∵2019÷4＝54…3，
∴点B2019与B3同在一个象限内，
∴点B2019（﹣22019，22019）．
故答案为（﹣22019，22019）．
字词句篇与同步作文达标系列答案【题目】在函数的学习中，我们经历了“确定函数表法式﹣画函数图象﹣利用函数图象研究函数性质﹣利用图象解决问题”的学习过程．在画函数图象时，我们常常通过描点或平移或翻折的方法画函数图象．小明根据学到的函数知识探究函数y1＝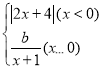
的图象与性质并利用图象解决问题．小明列出了如表y1与x的几组对应的值：
x | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
y1 | … | 4 | 2 | m | 2 | 4 | 2 |
| n |
| … |
（1）根据表格中x、y1的对应关系可得m＝______，n＝______；
（2）在平面直角坐标系中，描出表格中各点，两出该函数图象；根据函数图象，写出该函数的一条性质______．
（3）当函数y1的图象与直线y2＝mx+1有三个交点时，直接写出m的取值范围．
