ћвƒњƒЏ»Ё
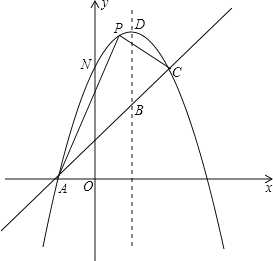
°Њћвƒњ°њ»зЌЉ£ђ“—÷™≈„ќпѕяy=©Бx2+bx+c”л“ї÷±ѕяѕаљї”ЏA(©Б1£ђ0)£ђC(2£ђ3)Ѕљµг£ђ”лy÷бљї”ЏµгN£Ѓ∆дґ•µгќ™D£Ѓ
£®1£©≈„ќпѕяЉ∞÷±ѕяACµƒЇѓ эєЎѕµ љ£ї
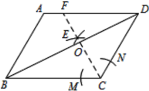
£®2£©»ф≈„ќпѕяµƒґ‘≥∆÷б”л÷±ѕяACѕаљї”ЏµгB£ђEќ™÷±ѕяAC…ѕµƒ»ќ“в“їµг£ђєэµгE„чEF°ќBDљї≈„ќпѕя”ЏµгF£ђ“‘B£ђD£ђE£ђFќ™ґ•µгµƒЋƒ±я–ќƒ№Јсќ™∆љ––Ћƒ±я–ќ£њ»фƒ№£ђ«уµгEµƒ„ш±к£ї»ф≤їƒ№£ђ«лЋµ√чјн”…£ї
£®3£©»фP «≈„ќпѕя…ѕќї”Џ÷±ѕяAC…ѕЈљµƒ“їЄцґѓµг£ђ«у°чAPCµƒ√жїэµƒ„оіу÷µ£Ѓ
°Њір∞Є°њ£®1£©y=©Бx2+2x+3£ђy=x+1£ї£®2£©¬ъ„гћхЉюµƒµгEµƒ„ш±кќ™(0£ђ1)їт(![]() £ђ
£ђ![]() )їт(
)їт(![]() £ђ
£ђ![]() )£ї£®3£©√жїэµƒ„оіу÷µќ™
)£ї£®3£©√жїэµƒ„оіу÷µќ™![]() £Ѓ
£Ѓ
°Њљвќц°њ
£®1£©ЄщЊЁµгA£ђBµƒ„ш±к£ђјы”√іэґ®ѕµ эЈ®Љіњ…«у≥ц≈„ќпѕяЉ∞÷±ѕяACµƒЇѓ эєЎѕµ љ£ї
£®2£©јы”√≈дЈљЈ®Љ∞“їіќЇѓ эЌЉѕу…ѕµгµƒ„ш±кћЎ’ч£ђњ…«у≥цµгB£ђDµƒ„ш±к£ђ…иµгEµƒ„ш±кќ™£®x£ђx+1£©£ђЈ÷µгE‘ЏѕяґќAC…ѕЉ∞µгE‘ЏѕяґќAC£®їтCA£©—”≥§ѕя…ѕЅљ÷÷«йњцњЉ¬«£ЇҐўµ±µгE‘ЏѕяґќAC…ѕ ±£ђµгF‘ЏµгE…ѕЈљ£ђ”…BDµƒ≥§љбЇѕµгEµƒ„ш±књ…µ√≥цµгFµƒ„ш±кќ™£®x£ђx+3£©£ђ‘ўјы”√ґюіќЇѓ эЌЉѕу…ѕµгµƒ„ш±кћЎ’чњ…«у≥цxµƒ÷µ£ђљшґшњ…µ√≥цµгEµƒ„ш±к£їҐЏµ±µгE‘ЏѕяґќAC£®їтCA£©—”≥§ѕя…ѕ ±£ђµгF‘ЏµгEѕ¬Јљ£ђ”…BDµƒ≥§љбЇѕµгEµƒ„ш±књ…µ√≥цµгFµƒ„ш±кќ™£®x£ђx©Б1£©£ђ‘ўјы”√ґюіќЇѓ эЌЉѕу…ѕµгµƒ„ш±кћЎ’чњ…«у≥цxµƒ÷µ£ђљшґшњ…µ√≥цµгEµƒ„ш±к£Ѓ„џ…ѕ£ђіЋќ µ√љв£ї
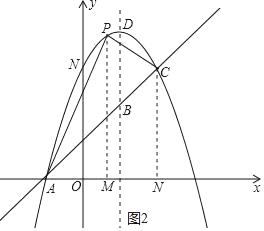
£®3£©єэµгP„чPM°Ќx÷б£ђіє„гќ™µгM£ђєэµгC„чCN°Ќx÷б£ђіє„гќ™N£ђ…иµгPµƒ„ш±кќ™£®x£ђ©Бx2+2x+3£©£®©Б1£Љx£Љ2£©£ђ‘тµгMµƒ„ш±кќ™£®x£ђ0£©£ђљбЇѕµгA£ђCµƒ„ш±кЉ∞S°чAPC£љS°чAPM+SћЁ–ќPMNC©БS°чACN£ђњ…µ√≥цS°чAPCєЎ”ЏxµƒЇѓ эєЎѕµ љ£ђ‘ўјы”√ґюіќЇѓ эµƒ–‘÷ Љіњ…љвЊц„о÷µќ ћв£Ѓ
љв£Ї£®1£©љЂA£®©Б1£ђ0£©£ђC£®2£ђ3£©іъ»лy£љ©Бx2+bx+c£ђµ√£Ї
![]() £ђљвµ√£Ї
£ђљвµ√£Ї![]() £ђ
£ђ
°а≈„ќпѕяµƒЇѓ эєЎѕµ љќ™y£љ©Бx2+2x+3£Ѓ
…и÷±ѕяACµƒЇѓ эєЎѕµ љќ™y£љkx+a£®k°ў0£©£ђ
љЂA£®©Б1£ђ0£©£ђC£®2£ђ3£©іъ»лy£љkx+a£ђµ√£Ї
![]() £ђљвµ√£Ї
£ђљвµ√£Ї![]() £ђ
£ђ
°а÷±ѕяACµƒЇѓ эєЎѕµ љќ™y£љx+1£Ѓ
£®2£©°яy£љ©Бx2+2x+3£љ©Б£®x©Б1£©2+4£ђ
°аµгDµƒ„ш±кќ™£®1£ђ4£©£Ѓ
µ±x£љ1 ±£ђy£љx+1£љ2£ђ
°аµгBµƒ„ш±кќ™£®1£ђ2£©£Ѓ
…иµгEµƒ„ш±кќ™£®x£ђx+1£©£Ѓ
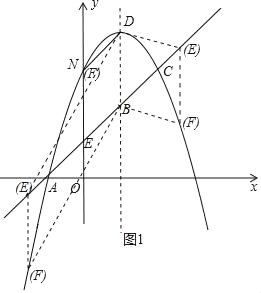
Ј÷Ѕљ÷÷«йњцњЉ¬«£®»зЌЉ1£©£Ї
Ґўµ±µгE‘ЏѕяґќAC…ѕ ±£ђµгF‘ЏµгE…ѕЈљ£ђ
°аµгFµƒ„ш±кќ™£®x£ђx+3£©£Ѓ
°яµгF‘Џ≈„ќпѕя…ѕ£ђ
°аx+3£љ©Бx2+2x+3£ђ
љвµ√£Їx1£љ0£ђx2£љ1£®…б»•£©£ђ
°аµгEµƒ„ш±кќ™£®0£ђ1£©£ї
ҐЏµ±µгE‘ЏѕяґќAC£®їтCA£©—”≥§ѕя…ѕ ±£ђµгF‘ЏµгEѕ¬Јљ£ђ
°аµгFµƒ„ш±кќ™£®x£ђx©Б1£©£Ѓ
°яµгF‘Џ≈„ќпѕя…ѕ£ђ
°аx©Б1£љ©Бx2+2x+3£ђ
љвµ√£Ї![]() £ђ
£ђ
°аµгEµƒ„ш±кќ™£®![]() £©їт£®
£©їт£®![]() £ђ
£ђ![]() £©£Ѓ
£©£Ѓ
„џ…ѕ£Ї¬ъ„гћхЉюµƒµгEµƒ„ш±кќ™£®0£ђ1£©£ђ£®![]() £©їт£®
£©їт£®![]() £ђ
£ђ![]() £©£Ѓ
£©£Ѓ
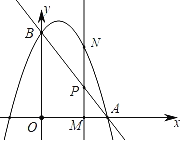
£®3£©єэµгP„чPM°Ќx÷б£ђіє„гќ™µгM£ђєэµгC„чCN°Ќx÷б£ђіє„гќ™N£ђ»зЌЉ2Ћщ Њ£Ѓ
…иµгPµƒ„ш±кќ™£®x£ђ©Бx2+2x+3£©£®©Б1£Љx£Љ2£©£ђ‘тµгMµƒ„ш±кќ™£®x£ђ0£©£Ѓ
°яµгAµƒ„ш±кќ™£®©Б1£ђ0£©£ђµгCµƒ„ш±кќ™£®2£ђ3£©£ђ
°аAM£љx+1£ђMN£љ2©Бx£ђPM£љ©Бx2+2x+3£ђCN£љ3£ђAN£љ3£ђ
°аS°чAPC£љS°чAPM+SћЁ–ќPMNC©БS°чACN£ђ
![]()
![]()
![]() £Ѓ
£Ѓ
![]()
°аµ±x£љ![]() ±£ђS°чAPC»°µ√„оіу÷µ£ђ„оіу÷µќ™
±£ђS°чAPC»°µ√„оіу÷µ£ђ„оіу÷µќ™![]() £ђіЋ ±µгPµƒ„ш±кќ™£®
£ђіЋ ±µгPµƒ„ш±кќ™£®![]() £©£Ѓ
£©£Ѓ

°Њћвƒњ°њ‘ЏЇѓ эµƒ—Іѕ∞÷–£ђќ“√«Њ≠јъЅЋ°∞»Јґ®Їѓ э±нЈ® љ©Бї≠Їѓ эЌЉѕу©Бјы”√Їѓ эЌЉѕу—–ЊњЇѓ э–‘÷ ©Бјы”√ЌЉѕуљвЊцќ ћв°±µƒ—Іѕ∞єэ≥ћ£Ѓ‘Џї≠Їѓ эЌЉѕу ±£ђќ“√«≥£≥£Ќ®єэ√иµгїт∆љ“∆їтЈ≠’џµƒЈљЈ®ї≠Їѓ эЌЉѕу£Ѓ–°√чЄщЊЁ—ІµљµƒЇѓ э÷™ ґћљЊњЇѓ эy1£љ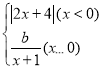 µƒЌЉѕу”л–‘÷ ≤Ґјы”√ЌЉѕуљвЊцќ ћв£Ѓ–°√чЅ–≥цЅЋ»з±нy1”лxµƒЉЄ„йґ‘”¶µƒ÷µ£Ї
µƒЌЉѕу”л–‘÷ ≤Ґјы”√ЌЉѕуљвЊцќ ћв£Ѓ–°√чЅ–≥цЅЋ»з±нy1”лxµƒЉЄ„йґ‘”¶µƒ÷µ£Ї
x | °≠ | ©Б4 | ©Б3 | ©Б2 | ©Б1 | 0 | 1 | 2 | 3 | 4 | °≠ |
y1 | °≠ | 4 | 2 | m | 2 | 4 | 2 |
| n |
| °≠ |
£®1£©ЄщЊЁ±нЄс÷–x°Ґy1µƒґ‘”¶єЎѕµњ…µ√m£љ______£ђn£љ______£ї
£®2£©‘Џ∆љ√ж÷±љ«„ш±кѕµ÷–£ђ√и≥ц±нЄс÷–Єчµг£ђЅљ≥цЄ√Їѓ эЌЉѕу£їЄщЊЁЇѓ эЌЉѕу£ђ–і≥цЄ√Їѓ эµƒ“їћх–‘÷ ______£Ѓ
£®3£©µ±Їѓ эy1µƒЌЉѕу”л÷±ѕяy2£љmx+1”–»эЄцљїµг ±£ђ÷±љ”–і≥цmµƒ»°÷µЈґќІ£Ѓ