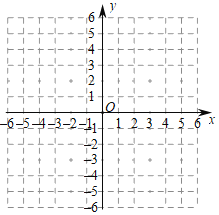题目内容
【题目】从甲地到乙地,先是一段上坡路,然后是一段平路,小明骑车从甲地出发,到达乙地后休息一段时间,然后原路返回甲地.假设小明骑车在上坡、平路、下坡时分别保持匀速前进,已知小明骑车上坡的速度比平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km,设小明出发xh后,到达离乙地ykm的地方,图中的折线ABCDEF表示y与x之间的函数关系.
(1)小明骑车在平路上的速度为 km/h,他在乙地休息了 h.
(2)分别求线段AB、EF所对应的函数关系式.
(3)从甲地到乙地经过丙地,如果小明两次经过丙地的时间间隔为0.85h,求丙地与甲地之间的路程.
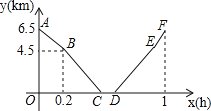
【答案】(1)15;0.1
(2)y=20x﹣13.5(0.9≤x≤1)
(3)丙地与甲地之间的路程为1千米
【解析】
(1)分别计算出小明骑车上坡的速度,小明平路上的速度,小明下坡的速度,小明平路上所用的时间,小明下坡所用的时间为,即可解答.
(2)根据上坡的速度为10km/h,下坡的速度为20km/h,所以线段AB所对应的函数关系式为:y=6.5-10x,线段EF所对应的函数关系式为y=4.5+20(x-0.9),即可解答.
(3)设小明出发a小时第一次经过丙地,根据题意得到6.5-10a=20(a+0.85)-13.5,求出a的值,即可解答.
(1)小明骑车上坡的速度为:(6.5﹣4.5)÷0.2=10(km/h),
小明平路上的速度为:10+5=15(km/h),
小明下坡的速度为:15+5=20(km/h),
小明平路上所用的时间为:2(4.5÷15)=0.6h,
小明下坡所用的时间为:(6.5﹣4.5)÷20=0.1h
所以小明在乙地休息了:1﹣0.1﹣0.6﹣0.2=0.1(h).
故答案为:15,0.1;
(2)由题意可知:上坡的速度为10km/h,下坡的速度为20km/h,
所以线段AB所对应的函数关系式为:y=6.5﹣10x,
即y=﹣10x+6.5(0≤x≤0.2).
线段EF所对应的函数关系式为y=4.5+20(x﹣0.9).
即y=20x﹣13.5(0.9≤x≤1).
(3)由题意可知:小明第一次经过丙地在AB段,第二次经过丙地在EF段,
设小明出发a小时第一次经过丙地,
则小明出发后(a+0.85)小时第二次经过丙地,
6.5﹣10a=20(a+0.85)﹣13.5
解得:a=![]() .
.
![]() =1(千米).
=1(千米).
答:丙地与甲地之间的路程为1千米.

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案【题目】在函数的学习中,我们经历了“确定函数表法式﹣画函数图象﹣利用函数图象研究函数性质﹣利用图象解决问题”的学习过程.在画函数图象时,我们常常通过描点或平移或翻折的方法画函数图象.小明根据学到的函数知识探究函数y1=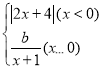 的图象与性质并利用图象解决问题.小明列出了如表y1与x的几组对应的值:
的图象与性质并利用图象解决问题.小明列出了如表y1与x的几组对应的值:
x | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
y1 | … | 4 | 2 | m | 2 | 4 | 2 |
| n |
| … |
(1)根据表格中x、y1的对应关系可得m=______,n=______;
(2)在平面直角坐标系中,描出表格中各点,两出该函数图象;根据函数图象,写出该函数的一条性质______.
(3)当函数y1的图象与直线y2=mx+1有三个交点时,直接写出m的取值范围.