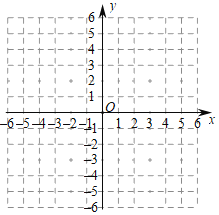题目内容
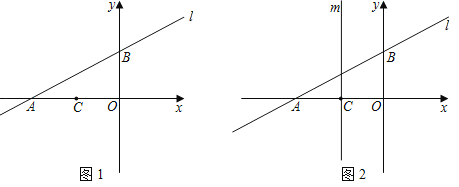
【题目】如图1,直线l:y=![]() x+2与x轴交于点A,与y轴交于点B.已知点C(﹣2,0).
x+2与x轴交于点A,与y轴交于点B.已知点C(﹣2,0).
(1)求出点A,点B的坐标.
(2)P是直线AB上一动点,且△BOP和△COP的面积相等,求点P坐标.
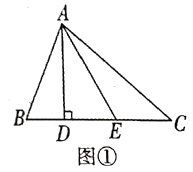
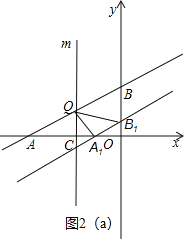
(3)如图2,平移直线l,分别交x轴,y轴于交于点A1,B1,过点C作平行于y轴的直线m,在直线m上是否存在点Q,使得△A1B1Q是等腰直角三角形?若存在,请直接写出所有符合条件的点Q的坐标.
【答案】(1)点A的坐标为(﹣4,0),点B的坐标的坐标为(0,2);(2)点P坐标为(4,4);(3)点Q为(﹣2,2)或(﹣2,﹣2)或(﹣2,-4)或(﹣2,![]() ).
).
【解析】
(1)根据求与![]() 轴交点坐标的方法,列出方程即可得到结论;
轴交点坐标的方法,列出方程即可得到结论;
(2)设![]() ,根据面积公式列出方程即可得出结论;
,根据面积公式列出方程即可得出结论;
(3)如图2,①当点![]() 是直角顶点时,根据全等三角形的性质即可得出结论;②当点
是直角顶点时,根据全等三角形的性质即可得出结论;②当点![]() 是直角顶点时,
是直角顶点时,![]() ,根据平移的性质得到直线
,根据平移的性质得到直线![]() 的解析式为
的解析式为![]() ,根据两点间的距离公式即可得到结论;③当点
,根据两点间的距离公式即可得到结论;③当点![]() 是直角顶点时,过点
是直角顶点时,过点![]() 作
作![]() 轴于点
轴于点![]() ,根据全等三角形的性质即可得出结论.
,根据全等三角形的性质即可得出结论.
解:(1)设y=0,则![]() x+2=0,
x+2=0,
解得:x=﹣4,
设x=0,则y=2,
∴点A的坐标为(﹣4,0),点B的坐标的坐标为(0,2);
(2)∵点C(﹣2,0),点B(0,2),
∴OC=2,OB=2,
∵P是直线AB上一动点,
∴设P(m,![]() m+2),
m+2),
∵△BOP和△COP的面积相等,
∴![]() ×2|m|=
×2|m|=![]() 2×(
2×(![]() |m|+2),
|m|+2),
解得:m=±4,
当m=﹣4时,点P与点A重合,
∴点P坐标为(4,4);
(3)存在;
理由:如图1,
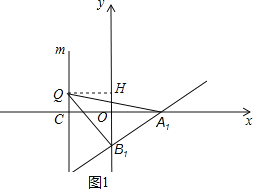
①当点B1是直角顶点时,
∴B1Q=B1A1,
∵∠A1B1O+∠QB1H=90°,∠A1B1O+∠OA1B1=90°,
∴∠OA1B1=∠QB1H,
在△A1OB1和△B1HQ中,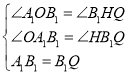 ,
,
∴△A1OB1≌△B1HQ(AAS),
∴B1H=A1O,OB1=HQ=2,
∴B1(0,﹣2)或(0,2),
当点B1(0,﹣2)时,Q(﹣2,2),
当点B1(0,2)时,
∵B(0,2),
∴点B1(0,2)(不合题意舍去),
∴Q(﹣2,2),
②当点A1是直角顶点时,A1B1=A1Q,
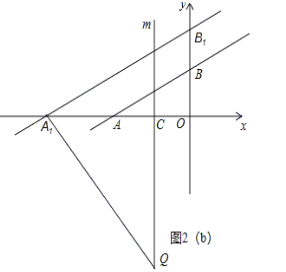
∵直线AB的解析式为y=![]() x+2,
x+2,
由平移知,直线A1B1的解析式为y=![]() x+b,
x+b,
∴A1(﹣2b,0),B1(0,b),
∴A1B12=4b2+b2=5b2,
∵A1B1⊥A1Q,
∴直线A1Q的解析式为y=﹣2x﹣4b
∴Q(﹣2,4﹣4b),
∴A1Q2=(﹣2b+2)2+(4﹣4b)2=20b2-40b+20,
∴20b2﹣40b+20=5b2,
∴b=2或b=![]() ,
,
∴Q(﹣2,-4)或(﹣2,![]() );
);
③当Q是直角顶点时,过Q作QH⊥y轴于H,

∴A1Q=B1Q,
∵∠QA1C1+∠A1QC=90°,∠A1QC+∠CQB1=90°,
∴∠QA1C=∠CQB1,
∵m∥y轴,
∴∠CQB1=∠QB1H,
∴∠QA1C=∠QB1H
在△A1QC与△B1QH中,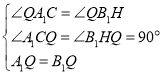 ,
,
∴△A1QC≌△B1QH(AAS),
∴CQ=QH=2,B1H=A1C,
∴Q(﹣2,2)或(﹣2,﹣2),
即:满足条件的点Q为(﹣2,2)或(﹣2,﹣2)或(﹣2,-4)或(﹣2,![]() ).
).

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案【题目】在函数的学习中,我们经历了“确定函数表法式﹣画函数图象﹣利用函数图象研究函数性质﹣利用图象解决问题”的学习过程.在画函数图象时,我们常常通过描点或平移或翻折的方法画函数图象.小明根据学到的函数知识探究函数y1=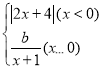 的图象与性质并利用图象解决问题.小明列出了如表y1与x的几组对应的值:
的图象与性质并利用图象解决问题.小明列出了如表y1与x的几组对应的值:
x | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
y1 | … | 4 | 2 | m | 2 | 4 | 2 |
| n |
| … |
(1)根据表格中x、y1的对应关系可得m=______,n=______;
(2)在平面直角坐标系中,描出表格中各点,两出该函数图象;根据函数图象,写出该函数的一条性质______.
(3)当函数y1的图象与直线y2=mx+1有三个交点时,直接写出m的取值范围.