题目内容
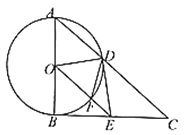
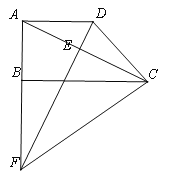
【题目】如图,已知梯形ABCD中,AD//BC ,∠ABC=90°,BC=2AB=8,对角线AC平分∠BCD,过点D作DE⊥AC,垂足为点E,交边AB的延长线于点F,联结CF.
(1)求腰DC的长;
(2)求∠BCF的余弦值.
【答案】(1)5;(2) ![]() .
.
【解析】
(1)根据勾股定理求出AC,求出CE,解直角三角形求出DE,根据勾股定理求出DC即可;
(2)根据相似三角形的性质和判定求出AF,求出CF,解直角三角形求出即可.
(1)∵∠ABC=90°,BC=2AB=8,∴AB=4,![]() .
.
∵AD//BC , ∴![]() .
.
∵AC平分∠BCD,∴![]() . ∴
. ∴![]() .
.
∴AD=CD.
∵DE⊥AC,∴![]() .
.
在Rt△![]() 中,
中,![]() ,
,![]() .
.
在Rt△![]() 中,
中,![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() ,
,![]() .
.
∴![]() .即腰DC的长是5.
.即腰DC的长是5.
(2)设DF与BC相交于点Q,
∵![]() ,
,![]() ,∴
,∴![]() .
.
∵![]() ,∴△
,∴△![]() ∽△
∽△![]() .∴
.∴![]() .
.
∵![]() ,
,![]() ,∴
,∴![]() ,即
,即![]() .
.
∵![]() ,
,![]() ,∴
,∴![]() .
.
在Rt△![]() 中,
中,![]() ,∴
,∴![]() .
.
即![]() 的余弦值是
的余弦值是![]() .
.

练习册系列答案
相关题目