题目内容
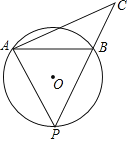
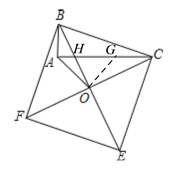
【题目】如图所示，以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF，设正方形的中心为O，连接AO，如果AB=4，AO=6
，那么AC=_____．
【答案】16．
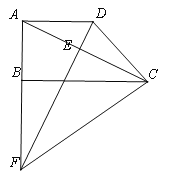
【解析】如图，在AC上取一点G，使CG=AB=4，连接OG，
∵四边形BCEF是正方形，对角线BE、CF相交于点O，
∴∠CBF=∠BOC=90°，
∴∠ABO=90°-∠AHB，∠OCG=90°-∠OHC，
又∵∠OHC=∠AHB，
∴∠ABO=∠OCG，
∵OB=OC，CG=AB
∴△OGC≌△OAB
∴OG=OA=
，∠BOA=∠GOC
∵∠GOC+∠GOH=90°，
∴∠GOH+∠BOA=90°
即：∠AOG=90°
∴△AOG是等腰直角三角形，
∴AG=
，
∴AC=AG+CG=12+4=16．
故选B．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
