题目内容
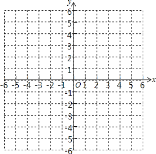
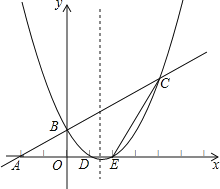
【题目】如图,已知一次函数y=![]() x+1的图象与x轴交于A点,与y轴交于B点:抛物线y=
x+1的图象与x轴交于A点,与y轴交于B点:抛物线y=![]() x2+bx+c的图象与一次函数y=
x2+bx+c的图象与一次函数y=![]() x+1的图象交于B、C两点,与x轴交于D、E两点,且点D的坐标为(1,0).
x+1的图象交于B、C两点,与x轴交于D、E两点,且点D的坐标为(1,0).
(1)求点B的坐标;
(2)求该抛物线的解析式;
(3)求四边形BDEC的面积S;
(4)在x轴上是否存在点P,使得以点P、B、C为顶点的三角形是直角三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
【答案】(1)B(0,1);(2)y=![]() x2-
x2-![]() x+1;(3)4.5;(4)点P的坐标为(
x+1;(3)4.5;(4)点P的坐标为(![]() ,0)或(
,0)或(![]() ,0)或(1,0)或(3,0).
,0)或(1,0)或(3,0).
【解析】
(1)在一次函数y=![]() x+1中,令x=0,即可求出点B的坐标;
x+1中,令x=0,即可求出点B的坐标;
(2)将点B、D的坐标代入二次函数解析式,求出b、c的值,即可求出二次函数的解析式;
(3)两解析式联立方程求得B、C的坐标,令y=![]() x2-
x2-![]() x+1=0,求得D、E的坐标,然后根据梯形和三角形的面积公式求得即可;
x+1=0,求得D、E的坐标,然后根据梯形和三角形的面积公式求得即可;
(4)设P(x,0),求得PB2=x2+1,PC2=(x-4)2+9,BC2=42+(3-1)2=20,然后分三种情况分别讨论求得即可.
(1)∵一次函数y=![]() x+1与y轴的交点为B,
x+1与y轴的交点为B,
令x=0,可得y=1,
∴B(0,1);
(2)将B(0,1),D(1,0)的坐标代入y=![]() x2+bx+c得,
x2+bx+c得,
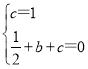 ,
,
解得: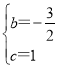 ,
,
∴解析式为:y=![]() x2-
x2-![]() x+1;
x+1;
(3)∵二次函数的图象与一次函数的图象交于B、C两点,
∴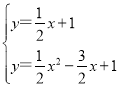 ,
,
解得:![]() ,
,![]() ,
,
∴C(4,3),
解![]() x2-
x2-![]() x+1=0,得x=1和x=2,
x+1=0,得x=1和x=2,
∴D(1,0),E(2,0),
∴S=![]() (1+3)×4-
(1+3)×4-![]() ×1×1-
×1×1-![]() (4-2)×3=4.5;
(4-2)×3=4.5;
(4)设P(x,0),
∵B(0,1),C(4,3),
∴PB2=x2+1,PC2=(x-4)2+9,BC2=42+(3-1)2=20,
①当∠PBC=90°时,则PB2+BC2=PC2,
即x2+1+20=(x-4)2+9,
解得x=![]() ,
,
∴P1(![]() ,0);
,0);
②当∠PCB=90°时,则PC2+BC2=PB2,
即x2+1=(x-4)2+9+20,
解得x=![]() ,
,
∴P2(![]() ,0);
,0);
③当∠BPC=90°时,则PB2+PC2=BC2,
即x2+1+(x-4)2+9=20,
解得x=1或x=3,
∴P3(1,0),P4(3,0);
∴在x轴上存在点P,使得以点P、B、C为顶点的三角形是直角三角形,点P的坐标为(![]() ,0)或(
,0)或(![]() ,0)或(1,0)或(3,0).
,0)或(1,0)或(3,0).

【题目】已知函数![]() ,如表是函数的几组对应值:
,如表是函数的几组对应值:
x |
|
|
|
|
|
| 0 | 1 | 2 | 3 |
| 4 |
|
y |
|
|
|
|
|
| 0 |
|
|
|
|
|
|
请你根据学习函数的经验,利用表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行探究![]() 下面是小腾的探究过程,请补充完整.
下面是小腾的探究过程,请补充完整.
![]() 如图所示,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点
如图所示,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点![]() 根据描出的点,画出该函数的图象
根据描出的点,画出该函数的图象
![]() 根据函数图象,按要求填空:
根据函数图象,按要求填空:
![]() 在y轴左侧该函数图象有最______点,其坐标为______.
在y轴左侧该函数图象有最______点,其坐标为______.
![]() 当
当![]() 时,该函数y随x的增大而______.
时,该函数y随x的增大而______.
![]() 当方程
当方程![]() 只有一个解时,则a的取值范围为______.
只有一个解时,则a的取值范围为______.